Question

【题目】在平面直角坐标系中，抛物线y＝﹣x2+x+m﹣1交x轴于A、B两点，交y轴于点C，若A点坐标为(x1，0)，B点坐标为(x2，0)（x1≠x2）．

（1）求m的取值范围；

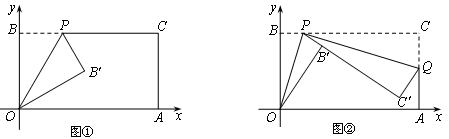
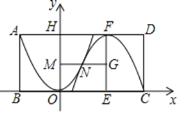
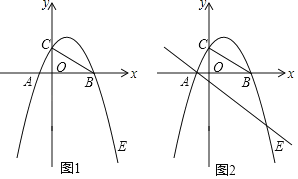
（2）如图1，若x12+x22＝17，求抛物线的解析式；

（3）在（2）的条件下，请解答下列两个问题：

①如图1，请连接AC，求证：△ACB为直角三角形．

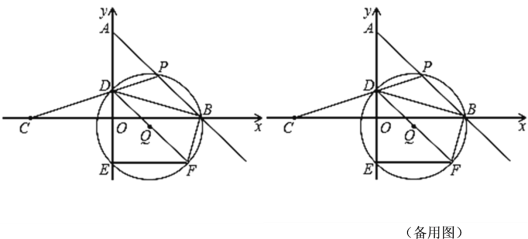
②如图2，若D(1，n)在抛物线上，过点A的直线y＝﹣x﹣1交（2）中的抛物线于点E，那么在x轴上点B的左侧是否存在点P，使以P、B、D为顶点的三角形与△ABE相似？若存在，求出P点坐标；若不存在，说明理由．

Answer 1

【答案】（1）m＞﹣；（2）y＝﹣x2+x+2；（3）①见解析；②存在，P(，0)或(﹣，0)

【解析】

（1）利用根的判别式，若有两个实根，则；

（2）利用一元二次方程两根与系数的关系，又x12+x22＝17，即可求解；

（3）①求出A，B，C三点坐标，计算得出AC2＝5，BC2＝20，AB2＝25，根据勾股定理逆定理即可求解；

②分△PBD∽△BAE、△PBD∽△EAB两种情况，分别求解即可．

解：（1）△＝（）2﹣4×（﹣）（m﹣1）＝+2m﹣2＝2m+，

由题可得2m+＞0，

∴m＞﹣；

（2）∵x1+x2＝3，x1x2＝﹣2（m﹣1），

又x12+x22＝17，

∴（x1+x2）2﹣2x1x2＝17∴32+4（m﹣1）＝17，

∴m＝3，

∴抛物线的解析式为y＝﹣x2+x+2；

（3）①证明：令y＝0，﹣x2+x+2＝0，

∴x1＝﹣1，x2＝4，

∴（﹣1，0），B（4，0）

令x＝0，y＝2，

∴C（0，2），

∴AC2＝5，BC2＝20，AB2＝25

∴AC2+BC2＝AB2∴△ACB为直角三角形；

②根据抛物线的解析式易知：D（1，3），

联立直线AE、抛物线解析式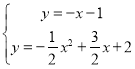：，解得或，

∴E（6，﹣7），

∴tan∠DBO＝1，即∠DBO＝45°，tan∠EAB＝1，即∠EAB＝45°，

∴∠DBA＝∠EAB，

若以P、B、D为顶点的三角形与△ABE相似，则有两种情况：

①△PBD∽△BAE； ②△PBD∽△EAB．

易知BD＝3，EA＝7，AB＝5，

由①得：，即，即.

由②得：，即，即PB＝，OP＝OB﹣BP＝﹣，

∴P（，0）或（﹣，0）．