题目内容
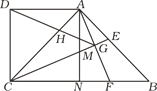
【题目】如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(0,4),点B的坐标为(4,0),点C的坐标为(﹣4,0),点P在AB上,连结CP与y轴交于点D,连结BD.过P,D,B三点作⊙Q与y轴的另一个交点为E,延长DQ交⊙Q于点F,连结EF,BF.
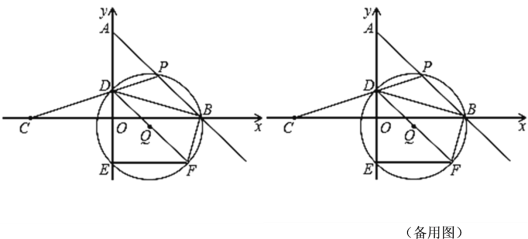
(1)求直线AB的函数解析式;
(2)求证:∠BDE=∠ADP;
(3)设DE=x,DF=y.请求出y关于x的函数解析式;
【答案】(1)y=﹣x+4;(2)详见解析;(3)y=![]() x
x
【解析】
(1)设直线AB的函数解析式为y=kx+4,把点B的坐标(4,0)代入即可;
(2)先证出△BDO≌△COD,得出∠BDO=∠CDO,再根据∠CDO=∠ADP,即可得出∠BDE=∠ADP;
(3)先连结PE,根据三角形外角的性质得∠ADP=∠DEP+∠DPE,∠BDE=∠ABD+∠OAB,由圆周角定理得∠DEP=∠ABD,由(2)知∠ADP=∠BDE,得出∠DPE=∠OAB,再证出∠DFE=∠DPE=45°,由直径所对的圆周角是直角得∠DEF=90°,得出△DEF是等腰直角三角形,从而求出DF=![]() DE,即y=
DE,即y=![]() x.
x.
解:(1)设直线AB的函数解析式为y=kx+4,
代入点B(4,0)得:4k+4=0,
解得:k=﹣1,
则直线AB的函数解析式为y=﹣x+4;

(2)由已知得:
OB=OC,∠BOD=∠COD=90°,
又∵OD=OD,
∴△BOD≌△COD,
∴∠BDO=∠CDO,
∵∠CDO=∠ADP,
∴∠BDE=∠ADP;
(3)连结PE,

∵∠ADP是△DPE的一个外角,
∴∠ADP=∠DEP+∠DPE,
∵∠BDE是△ABD的一个外角,
∴∠BDE=∠ABD+∠OAB,
∵∠ADP=∠BDE,∠DEP=∠ABD,
∴∠DPE=∠OAB,
∵OA=OB=4,∠AOB=90°,
∴∠OAB=45°,
∴∠DPE=45°,
∴∠DFE=∠DPE=45°,
∵DF是⊙Q的直径,
∴∠DEF=90°,
∴△DEF是等腰直角三角形,
∴DF=![]() DE,即y=
DE,即y=![]() x;
x;