题目内容
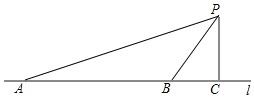
【题目】汽车超速行驶是交通安全的重大隐患,为了有效降低交通事故的发生,许多道路在事故易发路段设置了区间测速,如图新建的醴陵320国道(用直线l表示),进入株洲城区的AB路段设有区间测速,所有车辆限速60千米/小时(约为16.7米/秒),数学实践活动小组设计了如下活动:在l上确定A,B两点,并在AB路段进行区间测速.在l外取一点P,作PC⊥l,垂足为点C.测得PC=40米,∠APC=71°,∠BPC=35°.
(1)求AB的长;
(2)若上午9时测得一汽车从点A到点B用时5.5秒,请你用所学的数学知识说明该车是否超速.(参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70,sin71°≈0.95,cos71°≈0.33,tan71°≈2.90)
【答案】(1)AB的长约为88米;(2)该车没有超速,见解析
【解析】
(1)由三角函数定义求出AC、BC,即可得出答案;
(2)求出该汽车的速度,即可得出结论.
解:(1)在Rt△APC中,∠APC=71°,
∵tan∠APC=tan71°=![]() ≈2.90,
≈2.90,
∴AC≈40×2.90=116(米),
在Rt△BPC中,∠BPC=35°,
∵tan∠BPC=![]() tan35°=≈0.70,
tan35°=≈0.70,
∴BC≈40×0.70=28(米)
∴AB=AC﹣BC=116﹣28=88 (米);
答:AB的长约为88米;
(2)该汽车的速度约为:![]() =16m/s<16.7m/s,
=16m/s<16.7m/s,
∴该车没有超速.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目