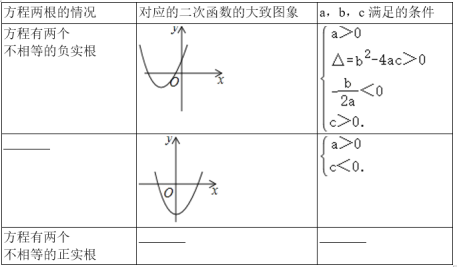
题目内容
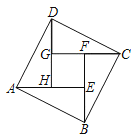
【题目】中国古代三国时期的数学家赵爽,创作了一幅“勾股弦方图”,通过数形结合,给出了勾股定理的详细证明如图,在“勾股弦方图”中,以弦为边长得到的正方形ABCD是由4个全等的直角三角形和中间的小正方形组成,这一图形被称作“赵爽弦图”张天同学要用细塑料棒制作“赵爽弦图”,若正方形ABCD与正方形EFCH的面积分别为169和49,则所用细塑料棒的长度为______.
【答案】100
【解析】
根据正方形的面积可得两个正方形的边长分别为13和7,再根据勾股定理可求得直角三角形的两条直角边长,进而求解.
∵正方形ABCD是由4个全等的直角三角形和中间的小正方形组成,
∴AE=BF,∠AEB=90°,
∵正方形ABCD与正方形EFCH的面积分别为169和49,
∴AB=13,EF=7,
在Rt△ABE中,BE=BF﹣EF=AE﹣7
根据勾股定理,得
AE2+BE2=AB2,
即AE2+(AE﹣7)2=132
解得,AE=12,
所以BE=12﹣7=5,
所以所用细塑料棒的长度为:4(AB+AE)=4(13+12)=100.
故答案为100.

练习册系列答案
相关题目