Question

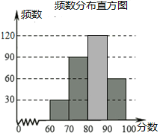
【题目】某校举行了“禁毒知识竞赛”活动，并随即抽查了部分同学的成绩，整理并制作成图表如下：

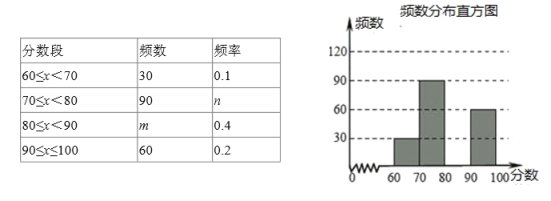
根据以上图表提供的信息，解答下列问题：

（1）请求出： ， ，抽查的总人数为 人；

（2）请补全频数分布直方图；

（3）抽查成绩的中位数应落在 分数段内；

（4）如果比赛成绩在80分以上（含80分）为优秀，任意抽取一位同学，则成绩优秀的概率为多少？

Answer 1

【答案】（1）120,0.3,300；（2）图见解析；（3）；（4）60%

【解析】

（1）用第一组的频数除以频率求出样本容量，用样本容量乘以第三组的频率，用第二组的频数除以样本容量即可求出答案；

（2）根据m的值即可把直方图补充完整；

（3）根据中位数的定义直接得出中位数应落在80≤x＜90分数段内；

（4）用比赛成绩80分以上的频数除以样本容量即可．

（1）本次调查的样本容量为30÷0.1=300，

则m=300×0.4=120，

n=90÷300=0.3，

故答案为：120，0.3，300；

（2）频数分布直方图如图：

（3）∵共有300名学生参加知识竞赛，最中间的数是第150和151个数的平均数，

∴中位数应落在80≤x＜90分数段内，

故答案为：80≤x＜90；

（4）如果比赛成绩80分以上为优秀，

则该竞赛项目的优秀率 ．