题目内容
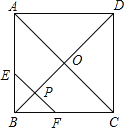
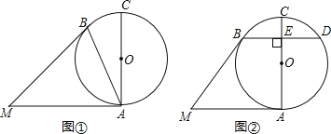
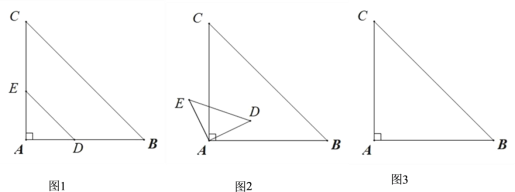
【题目】如图 1,在等腰直角△ABC 中,∠A =90°,AB=AC=3,在边 AB 上取一点 D(点 D 不与点 A,B 重合),在边 AC 上取一点 E,使 AE=AD,连接 DE. 把△ADE 绕点 A 逆时针方向旋转α(0°<α<360°),如图 2.
(1)请你在图 2 中,连接 CE 和 BD,判断线段 CE 和 BD 的数量关系,并说明理由;
(2)请你在图 3 中,画出当α =45°时的图形,连接 CE 和 BE,求出此时△CBE 的面积;
(3)若 AD=1,点 M 是 CD 的中点,在△ADE 绕点 A 逆时针方向旋转的过程中,线段AM 的最小值是 .
【答案】(1)CE=BD,理由见解析;(2)图形见解析,![]() ;(3)1.
;(3)1.
【解析】
(1)连接CE和BD,求出∠EAC=∠DAB,即可利用SAS证明△AEC≌△ADB,进而得到CE=BD;
(2)连接CE和BE,延长AD交BC于F,首先求出∠BAF=∠CAF=∠EAC=45°,然后可得AF=BF=CF,∠EAB=135°,进而证明AE∥BC,再根据![]() 进行计算;
进行计算;
(3)判断出在△ADE绕点A逆时针方向旋转的过程中,点M在以G为圆心,![]() 长为半径的圆上,即可得到点M与点E重合时AM取最小值.
长为半径的圆上,即可得到点M与点E重合时AM取最小值.
解:(1)CE=BD;
理由:连接CE和BD,如图2所示,
由题意可知,△ABC和△ADE都是等腰直角三角形,
∵∠EAD=∠CAB=90°,
∴∠EAC=∠DAB,
又∵AE=AD,AC=AB,
∴△AEC≌△ADB(SAS),
∴CE=BD;
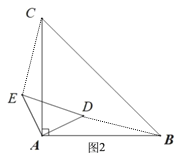
(2)当α =45°时,连接CE和BE,如图所示,延长AD交BC于F,
∵α =45°,△ABC和△ADE都是等腰直角三角形,
∴∠BAF=∠CAF=∠EAC=45°,
∴AF=BF=CF,∠EAB=135°,
∴∠EAB+∠ABC=135°+45°=180°,
∴AE∥BC,
∵BC=![]() ,
,
∴AF=![]() ,
,
∴![]() ;
;
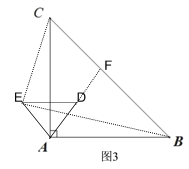
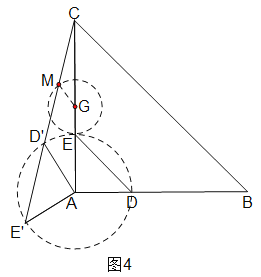
(3)如图4,当点M不在AC上时,取AC中点G,连接GM,
∵M是CD′的中点,
∴GM=![]() ,
,
当点M在AC上时,由M是CD′的中点可得GM=![]() ,
,
∴在△ADE绕点A逆时针方向旋转的过程中,点M在以G为圆心,![]() 长为半径的圆上,
长为半径的圆上,
∴当点M与点E重合时AM取最小值,此时AM=AE=1.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案