题目内容
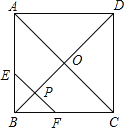
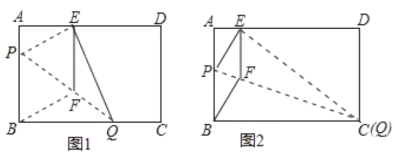
【题目】如图1，在矩形纸片
中，
，
，折叠纸片使
点落在边
上的
处，折痕为
，过点作
交于
，连接
．
（1）求证：四边形
为菱形；
（2）当点在边上移动时，折痕的端点
也随之移动；
①当点
与点
重合时（如图2），求菱形的边长；
②若限定分别在边
上移动，求出点在边上移动的最大距离．
【答案】（1）见解析；（2）①
，②
【解析】
（1）根据轴对称的性质得到
，
，
，再由平行线的性质得到
，从而得到
，由“等角对等边”得到EP=EF，进而得出
即可；
（2）①先由折叠得：EC＝BC＝10，利用勾股定理得：ED＝8，设PE＝x，则PB＝x，AP＝6x，Rt△APE中，由勾股定理得：（6x）2＋22＝x2，解出即可；
②当点Q与点C重合时，点E离点A最近，由①知，此时AE＝2cm；当点P与点A重合时，点E离点A最远，AE＝AB＝6cm，即可得出答案；
解：（1）证明：
折叠纸片使
点落在边
上的
处，折痕为
，
点与点关于对称，
，，，
又
，
，
，
，
，
四边形
为菱形；
（2）解：①四边形
是矩形，
，
，
，
点与点关于对称，点C与点Q重合，
，
在
中，
，
；
在
中，
，
，
，
解得：
，
菱形的边长为；
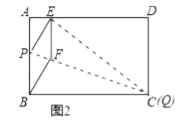
②当点
与点
重合时，如图2；
点离点
最近，由①知，此时
；
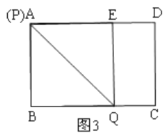
当点
与点重合时，如图3所示：
点离点最远，此时四边形
为正方形，
，
点在边上移动的最大距离为6-2=.
练习册系列答案
相关题目
