题目内容
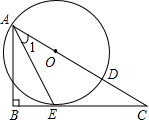
如图,已知AB是⊙O的直径,AC是弦,直线CE和⊙O切于点C,AD⊥CE,垂足为D.
求证:AC2=AD•AB.

求证:AC2=AD•AB.

证明:
连接OC,BC,
∵AB是⊙O直径,
∴∠BCA=90°,
∵DE切⊙O于C,
∴∠DCO=90°,
∴∠DCO-∠OCA=∠BCA-∠OCA,
∴∠DCA=∠OCB,
∵OC=OB,
∴∠B=∠OCB,
∴∠B=∠DCA,
∵AD⊥DE,
∴∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴
=
,
∴AC2=AD•AB.
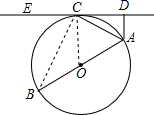
连接OC,BC,
∵AB是⊙O直径,
∴∠BCA=90°,
∵DE切⊙O于C,
∴∠DCO=90°,
∴∠DCO-∠OCA=∠BCA-∠OCA,
∴∠DCA=∠OCB,
∵OC=OB,
∴∠B=∠OCB,
∴∠B=∠DCA,
∵AD⊥DE,
∴∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴
| AC |
| AB |
| AD |
| AC |
∴AC2=AD•AB.


练习册系列答案
相关题目