题目内容
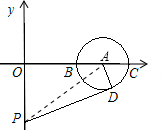
如图,⊙A与x轴交于B(2,0)、C(4,0)两点,OA=3,点P是y轴上的一个动点,PD切⊙O于点D,则PD的最小值是______.


连接AP,如图所示:
∵B(2,0)、C(4,0),
∴OB=2,OC=4,
∴BC=OC-OB=4-2=2,即圆A的直径为2,
∴AD=1,OA=OB+AB=2+1=3,
又∵DP为圆A的切线,
∴AD⊥DP,
∴∠ADP=90°,
设P(0,y),
在Rt△AOP中,OA=3,OP=|y|,
根据勾股定理得:AP2=OA2+OP2=9+y2,
在Rt△APD中,AD=1,
根据勾股定理得:PD2=AP2-AD2=9+y2-1=y2+8,
则PD=
,
则当y=0时,PD达到最小值,最小值为
=2
.
故答案为:2

∵B(2,0)、C(4,0),
∴OB=2,OC=4,
∴BC=OC-OB=4-2=2,即圆A的直径为2,
∴AD=1,OA=OB+AB=2+1=3,
又∵DP为圆A的切线,
∴AD⊥DP,
∴∠ADP=90°,
设P(0,y),
在Rt△AOP中,OA=3,OP=|y|,
根据勾股定理得:AP2=OA2+OP2=9+y2,
在Rt△APD中,AD=1,
根据勾股定理得:PD2=AP2-AD2=9+y2-1=y2+8,
则PD=
| y2+8 |
则当y=0时,PD达到最小值,最小值为
| 8 |
| 2 |
故答案为:2
| 2 |

练习册系列答案
相关题目





