题目内容
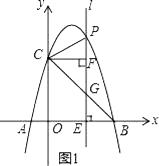
【题目】如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.
(1)求抛物线的表达式;
(2)当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;
(3)如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
【答案】
(1)
解:将点A(﹣1,0),B(4,0)的坐标代入函数的表达式得: ![]() ,解得:b=3,c=4.
,解得:b=3,c=4.
所以 抛物线的解析式为y=﹣x2+3x+4.
(2)
解:如图1所示:
∵令x=0得y=4,
∴OC=4.
∴OC=OB.
∵∠CFP=∠COB=90°,
∴FC=PF时,以P,C,F为顶点的三角形与△OBC相似.
设点P的坐标为(a,﹣a2+3a+4)(a>0).
则CF=a,PF=|﹣a2+3a+4﹣4|=|a2﹣3a|.
∴|a2﹣3a|=a.
解得:a=2,a=4.
∴点P的坐标为(2,6)或(4,0).
(3)
解:如图2所示:连接EC.
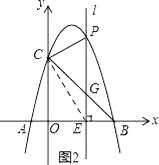
设点P的坐标为(a,﹣a2+3a+4).则OE=a,PE=﹣a2+3a+4,EB=4﹣a.
∵S四边形PCEB= ![]() OBPE=
OBPE= ![]() ×4(﹣a2+3a+4),S△CEB=
×4(﹣a2+3a+4),S△CEB= ![]() EBOC=
EBOC= ![]() ×4×(4﹣a),
×4×(4﹣a),
∴S△PBC=S四边形PCEB﹣S△CEB=2(﹣a2+3a+4)﹣2(4﹣a)=﹣2a2+8a.
∵二次项系数是﹣2<0,
∴当a=2时,△PBC的面积S有最大值.
∴P(2,6),△PBC的面积的最大值为8.
【解析】(1)二次函数的解析式中有两个未知数,根据两个点的坐标列方程组可解得两个未知数;
(2)由B(4,0),C(0,4)可得△OBC是等腰直角三角形,则△CPF也是等腰直角三角形,因为∠CFP=90度,则CF=PF,则根据它可列方程求得;
(3)设出点P的坐标(a,﹣a2+3a+4),用a表示出△PBC的面积,根据二次函数的最值问题求出最大值.

【题目】自行车厂某周计划生产2100辆电动车,平均每天生产电动车300辆.由于各种原因,实际每天的生产量与计划每天的生产量相比有出入,下表是该周的实际生产情况(超产记为正、减产记为负,单位:辆):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
减增 |
|
|
|
|
|
|
|
(1)该厂星期一生产电动车________辆;
(2)生产量最多的一天比生产量最少的一天多生产电动车________辆;
(3)该厂实行记件工资制,每生产一辆车可得60元,那么该厂工人这一周的工资总额是多少元?
【题目】观察下列一组勾股数:
|
|
| |
第1组 | 3=2×1+1 | 4=2×1×(1+1) | 5=2×1×(1+1)+1 |
第2组 | 5=2×2+1 | 12=2×2×(2+1) | 13=2×2×(2+1)+1 |
第3组 | 7=2×3+1 | 24=2×3×(3+1) | 25=2×3×(3+1)+1 |
第4组 | 9=2×4+1 | 40=2×4×(4+1) | 41=2×4×(4+1)+1 |
… | … | … | … |
观察以上各组勾股数的特点:
(1)请写出第7组勾股数![]() ,
,![]() ,
,![]() ;
;
(2)写出第![]() 组勾股数
组勾股数![]() ,
,,
![]() .
.