题目内容
【题目】如图,在直角坐标系中,矩形OABC的顶点A在x轴上,顶点C在y轴上,B(4,3),连接OB,将△OAB沿直线OB翻折,得△ODB,OD与BC相交于点E,若双曲线 ![]() 经过点E,则k= ;
经过点E,则k= ;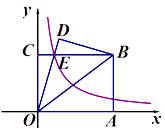
【答案】![]()
【解析】解:B点的坐标为(4,3),则OA=CB=4,OC=AB=3,
易知 ![]() OBD≌OBA,则∠D=∠OAB=90°,BD=OC=3.
OBD≌OBA,则∠D=∠OAB=90°,BD=OC=3.
四边形OABC是矩形,则∠OCB=90°,即∠OCB=∠D.
因为∠OEC=∠BED,所以 ![]() OEC≌
OEC≌ ![]() BED,CE=DE.
BED,CE=DE.
令CE=DE=x,则有: CE+BE=x+ ![]() =4,解得x=
=4,解得x= ![]() .
.
E点的坐标为( ![]() ,3).
,3).
双曲线过点E,则k= ![]() ×3=
×3= ![]() .
.
故答案为 ![]() .
.
双曲线过点E,关键是求出E点的坐标,已知B点的坐标是(4,3),显然E点和B点的纵坐标是相同的,即E点的纵坐标是3。 ![]() BOD由
BOD由 ![]() OBA折叠而来,所以二者是全等的,进而可以证明
OBA折叠而来,所以二者是全等的,进而可以证明 ![]() OEC≌
OEC≌ ![]() BED,CE=DE。从而求出CE的长度,即E点的横坐标。
BED,CE=DE。从而求出CE的长度,即E点的横坐标。

练习册系列答案
相关题目
【题目】学期结束前,学校想调查学生对七年级数学实验教材的意见,特向七年级400名学生作问卷调查,其结果如下:
(1)计算出每一种意见的人数占调查人数的百分比;
(2)从统计图中你能得出什么结论?
意见 | 非常喜欢 | 喜欢 | 有一点喜欢 | 不喜欢 |
人数 | 200 | 160 | 32 | 8 |