Question

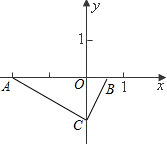
在平面直角坐标系内有两点A（-2，0），B（

1

2

，0），CB所在直线为y=2x+b，
（1）求b与C的坐标；
（2）连接AC，求证：△AOC∽△COB；
（3）求过A，B，C三点且对称轴平行于y轴的抛物线解析式；
（4）在抛物线上是否存在一点P（不与C重合），使得S_△ABP=S_△ABC？若存在，请求出P点坐标；若不存在，请说明理由．

Answer 1

（1）以B（

1

2

，0）代入y=2x+b，2×

1

2

+b=0，（2分）
得：b=-1则有C（0，-1）．（3分）

（2）∵OC⊥AB，且

|OB|

|OC|

=

|OC|

|OA|

=

1

2

，（5分）
∴△AOC∽△COB．（6分）

（3）设抛物线的解析式为y=ax²+bx+c，以三点的坐标代入解析式得方程组：

(- 1 2 )2a+ 1 2 b+c=0 (-2)2a+(-2)b+c=0 c=-1

?

a=1 b= 3 2 c=-1

，（8分）
所以y=x²+

3

2

x-1．（9分）

（4）假设存在点P（x，y）
依题意有

S△ABP

S△ABC

=

1 2 |AB|•|y|

1 2 |AB|•|OC|

=1，
得：|y|=|OC|=1．（10分）
①当y=1时，有x²+

3

2

x-1=1
即x²+

3

2

x-2=0，
解得：x1=

-3+ 41

4

，x2=

-3- 41

4

（11分）
②当y=-1时，有x²+

3

2

x-1=-1，
即x²+

3

2

x=0，
解得：x₃=0（舍去），x4=-

3

2

．
∴存在满足条件的点P，它的坐标为：(-

3

2

，-1)，(

-3+ 41

4

，1)，(

-3- 41

4

，1)．（12分）