题目内容
已知二次函数y=ax2+bx+c(a≠0)中自变量x和函数值y的部分对应值如下表:
(1)求二次函数解析式,并写出顶点坐标;
(2)在直角坐标系中画出该抛物线的图象
(3)若该抛物线上两点A(x1,y1)、B(x2,y2)的横坐标满足x1<x2<-1,试比较y1与y2的大小.
| x | … | -3 | -2 | -1 | 0 | 1 |
| y | … | -6 | 0 | 4 | 0 | 6 |
(2)在直角坐标系中画出该抛物线的图象
(3)若该抛物线上两点A(x1,y1)、B(x2,y2)的横坐标满足x1<x2<-1,试比较y1与y2的大小.
(1)
由图表可知抛物线y=ax2+bx+c过点(-2,0),(0,0),求出对称轴即可:
x=-1;
∴顶点坐标为:(-1,4),
∴设y=a(x+1)2+4,
将(0,0)代入可得:a+4=0,
解得:a=-4,
∴二次函数的解析式为:y=-4(x+1)2+4=-4x2-8x.
(2)由表格中的值可以判断:
图象与x轴交点坐标为:(-2,0),(0,0),顶点坐标为:(-1,4),
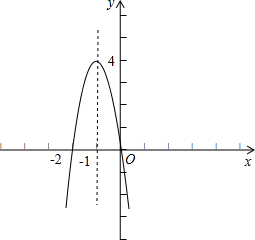
(3)∵该抛物线上两点A(x1,y1)、B(x2,y2)的横坐标满足x1<x2<-1,
∵x<-1时,y随x的增大而增大,
∵x1<x2<-1,
∴y1<y2.
| x | … | -3 | -2 | -1 | 0 | 1 |
| y | … | -6 | 0 | 4 | 0 | -6 |
x=-1;
∴顶点坐标为:(-1,4),
∴设y=a(x+1)2+4,
将(0,0)代入可得:a+4=0,
解得:a=-4,
∴二次函数的解析式为:y=-4(x+1)2+4=-4x2-8x.
(2)由表格中的值可以判断:
图象与x轴交点坐标为:(-2,0),(0,0),顶点坐标为:(-1,4),
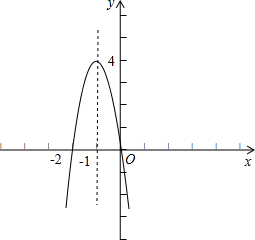
(3)∵该抛物线上两点A(x1,y1)、B(x2,y2)的横坐标满足x1<x2<-1,
∵x<-1时,y随x的增大而增大,
∵x1<x2<-1,
∴y1<y2.

练习册系列答案
相关题目
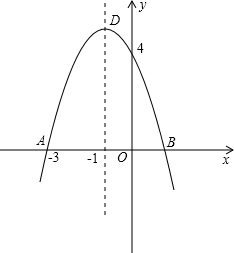 (-3,0),
(-3,0),