题目内容
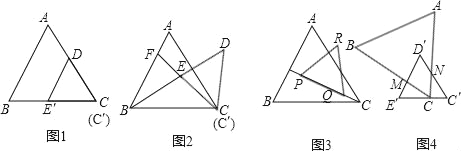
【题目】图1是边长分别为4
和3的两个等边三角形纸片ABC和C′D′E′叠放在一起（C与C′重合）．
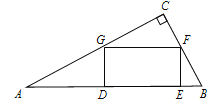
（1）操作：固定△ABC，将△C′D′E′绕点C顺时针旋转30°得到△CDE，连接AD、BE，CE的延长线交AB于F（图2）；
探究：在图2中，线段BE与AD之间有怎样的大小关系？试证明你的结论．
（2）操作：将图2中的△CDE，在线段CF上沿着CF方向以每秒1个单位的速度平移，平移后的△CDE设为△PQR（图3）；
请问：经过多少时间，△PQR与△ABC重叠部分的面积恰好等于
？
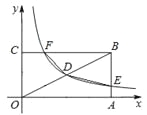
（3）操作：图1中△C′D′E′固定，将△ABC移动，使顶点C落在C′E′的中点，边BC交D′E′于点M，边AC交D′C′于点N，设∠AC C′＝α（30°＜α＜90，图4）；
探究：在图4中，线段C′NE′M的值是否随α的变化而变化？如果没有变化，请你求出C′NE′M的值，如果有变化，请你说明理由．
【答案】(1)见解析;(2) 1秒;(3)见解析.
【解析】
（1）由△ABC与△DCE是等边三角形，利用SAS易证得△BCE≌△ACD，即可得BE=AD；
（2）首先设经过x秒重叠部分的面积是
，在△CQT中，求得QT=QC=x，RT=3-x，根据三角形面积公式可得方程
×32-
（3-x）2=，解此方程即可求得答案；
（3）首先证得∠MCE′=∠CNC′，又由∠E′=∠C′，根据有两角对应相等的三角形相似证得△E′MC∽△C′CN，又由相似三角形的对应边成比例，即可求得答案．
（1）BE＝AD
证明：∵△ABC与△DCE是等边三角形，
∴∠ACB＝∠DCE＝60°，CA＝CB，CE＝CD，
∴∠BCE＝∠ACD，
∴△BCE≌△ACD，
∴BE＝AD；
（2）设经过x秒重叠部分的面积是，
如图在△CQT中，
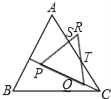
∵∠TCQ＝30°，∠RQP＝60°，
∴∠QTC＝30°，
∴∠QTC＝∠TCQ，
∴QT＝QC＝x，
∴RT＝3﹣x，
∵∠RTS+∠R＝90°，
∴∠RST＝90°，
由已知得×32-（3-x）2=，
∴x1＝1，x2＝5，
∵0≤x≤3，
∴x＝1，
答：经过1秒重叠部分的面积是；
（3）C′NE′M的值不变．
证明：∵∠ACB＝60°，
∴∠MCE′+∠NCC′＝120°，
∵∠CNC′+∠NCC′＝120°，
∴∠MCE′＝∠CNC′，
∵∠E′＝∠C′，
∴△E′MC∽△C′CN，
∴
，
∴C′NE′M＝C′CE′C＝
．
