题目内容
【题目】已知二次函数y=﹣x2+bx+c(b,c均为常数)的图象经过两点A(2,0),B(0,﹣6).
(1)求这个二次函数的解析式;
(2)若点C(m,0)(m>2)在这个二次函数的图象上,连接AB,BC,求△ABC的面积.
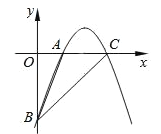
【答案】(1)y=﹣x2+5x﹣6;(2)3.
【解析】
(1)把A、B的坐标代入y=﹣x2+bx+c,即可求出函数解析式;
(2)求出C点的坐标,求出AC的值,根据三角形面积公式求出即可.
(1)把(2,0)(0,﹣6)代入y=﹣x2+bx+c,得:
![]() ,解得:b=5,c=﹣6,
,解得:b=5,c=﹣6,
∴二次函数的解析式y=﹣x2+5x﹣6;
(2)由(1)得二次函数的解析式为:y=﹣x2+5x﹣6,令y=0,即0=﹣x2+5x﹣6,解得:x1=2,x2=3.
∵m>2,
∴C(3,0),
∴AC=1,
∴S△ABC=![]() ACOB=
ACOB=![]() ×1×6=3,
×1×6=3,
∴△ABC的面积=3.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
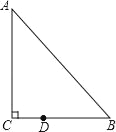
【题目】如图,在Rt△ABC中,∠C=90°,∠B=40°,点D在边BC上,BD=2CD,把△ABC绕点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,则m=_____.