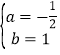Question

【题目】已知点D与点A（0，6）、B（0，﹣4）、C（x，y）是平行四边形的四个顶点，其中x、y满3x﹣4y+12＝0，则CD的最小值为_____．

Answer 1

【答案】

【解析】

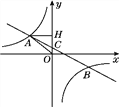
如图所示，根据平行四边形的性质可知：对角线AB、CD互相平分，可得CD过线段AB的中点M，即CM=DM，根据A与B坐标求出M坐标，要求CD的最小值只需求出CM的最小值即可．

根据平行四边形的性质可知：对角线AB、CD互相平分，

∴CD过线段AB的中点M，即CM=DM，

∵A（0，6），B（0，-4），

∴M（0，1），

∵点到直线的距离垂线段最短，

∴过M作直线CF的垂线交直线CF于点C，此时CM最小，

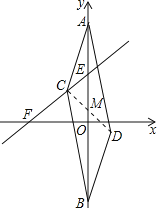
直线3x-4y+12=0，令x=0得到y=3；令y=0得到x=-4，即F（-4，0），E（0，3），

∴OE=3，OF=4，EM=2，EF==5，

∵△EOF∽△ECM，

∴，即，

解得：CM=，

则CD的最小值为．

故答案为：．