Question

【题目】在ABCD中，AB＜BC，已知∠B=30°，AB=，将△ABC沿AC翻折至△AB′C，使点B′落在ABCD所在的平面内，连接B′D．若△AB′D是直角三角形，则BC的长为 ．

Answer 1

【答案】4或6
【解析】解：当∠B′AD=90°AB＜BC时，如图1，
∵AD=BC，BC=B′C，
∴AD=B′C，
∵AC∥B′D，∠B′AD=90°，
∴∠B′GC=90°，
∵∠B=30°，AB=2，
∴∠AB′C=30°，
∴GC= B′C= BC，
∴G是BC的中点，
在Rt△ABG中，BG=AB=×2=3，
∴BC=6；
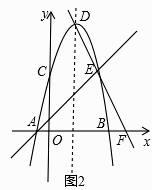
当∠AB′D=90°时，如图2，
∵AD=BC，BC=B′C，
∴AD=B′C，
∵AC∥B′D，
∴四边形ACDB′是等腰梯形，
∵∠AB′D=90°，
∴四边形ACDB′是矩形，
∴∠BAC=90°，
∵∠B=30°，AB=2，
∴BC=AB÷=2×=4，
∴当BC的长为4或6时，△AB′D是直角三角形．
所以答案是：4或6．


【考点精析】认真审题，首先需要了解平行四边形的性质(平行四边形的对边相等且平行；平行四边形的对角相等，邻角互补；平行四边形的对角线互相平分)，还要掌握翻折变换（折叠问题）(折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等)的相关知识才是答题的关键．