��Ŀ����
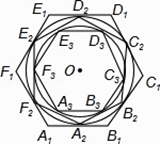
����Ŀ����ֱ֪��m��n����C��ֱ��m��һ�㣬��D��ֱ��n��һ�㣬CD��ֱ��m��n����ֱ����PΪ�߶�CD���е㣮
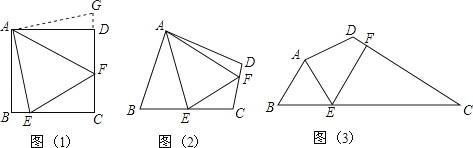
��1���������֣�ֱ��l��m��l��n������ֱ�ΪA��B������A���C�غ�ʱ����ͼ����ʾ��������PB����ֱ��д���߶�PA��PB��������ϵ�� ��
��2������֤������ͼ�ٵ�����£���ֱ��l����ƽ�Ƶ���ͼ�ڵ�λ�ã����ʣ�1���е�PA��PB�Ĺ�ϵʽ�Ƿ���Ȼ����������������֤����������������˵�����ɣ�
��3������̽������ͼ�ڵ�����£���ֱ��l�Ƶ�A��ת��ʹ�á�APB=90�㣨��ͼ����ʾ��������ƽ����m��n֮��ľ���Ϊ2k����֤��PAPB=kAB��
���𰸡�
��1��PA=PB
��2��
�⣺��ֱ��l����ƽ�Ƶ���ͼ�ڵ�λ�ã�PA=PB��Ȼ�������������£�
��ͼ�ڣ���C��CE��n�ڵ�E������PE��
 ��
��
��������CED��ֱ�������Σ���PΪ�߶�CD���е㣬
��PD=PE��
�֡ߵ�PΪ�߶�CD���е㣬
��PC=PD��
��PC=PE��
��PD=PE��
���CDE=��PEB��
��ֱ��m��n��
���CDE=��PCA��
���PCA=��PEB��
�֡�ֱ��l��m��l��n��CE��m��CE��n��
��l��CE��
��AC=BE��
�ڡ�PAC�͡�PBE�У�

���PAC�ա�PBE��
��PA=PB��
��3��
�⣺��ͼ�ۣ��ӳ�AP��ֱ��n�ڵ�F����AE��BD�ڵ�E��
 ��
��
��ֱ��m��n��
�� ![]() ��
��
��AP=PF��
�ߡ�APB=90�㣬
��BP��AF��
�֡�AP=PF��
��BF=AB��
�ڡ�AEF�͡�BPF�У�
![]()
���AEF�ס�BPF��
�� ![]() ��
��
��AFBP=AEBF��
��AF=2PA��AE=2k��BF=AB��
��2PAPB=2k��AB��
��PAPB=kAB��
��������������֤������ʱ��P��m��n�Ĵ��߷ֱ���G��S���㣬GP=k����PAm=��PFE=��PAB��APΪ��mAB�Ľ�ƽ���ߣ���ƽ�����ϵ�P�㵽�����ߵľ�����ȣ�����h=k���ɴ˼��ɽ�����⣬���ַ����Ƚϼ�
���������⣺��1����l��n��
��BC��BD��
��������CBD��ֱ�������Σ�
�֡ߵ�PΪ�߶�CD���е㣬
��PA=PB����2��
�����㾫����ͨ������������������ε����ʺ����������ε��ж������ն�Ӧ����ȣ���Ӧ�߳ɱ��������������ν������������Σ����������ε��ж�����:���Ƕ�Ӧ��ȣ������������ƣ�ASA����ֱ�������α�б���ϵĸ߷ֳɵ�����ֱ�������κ�ԭ���������ƣ� ���߶�Ӧ�ɱ����Ҽн���ȣ������������ƣ�SAS�������߶�Ӧ�ɱ����������������ƣ�SSS�������Խ����⣮

 ʱ�����������ҵԭ���ܳ�����ϵ�д�
ʱ�����������ҵԭ���ܳ�����ϵ�д� ����νӽ̲���ĩ���Ԥϰ�人������ϵ�д�
����νӽ̲���ĩ���Ԥϰ�人������ϵ�д� ������ҵ��ٳɳ����½������������ϵ�д�
������ҵ��ٳɳ����½������������ϵ�д�