��Ŀ����
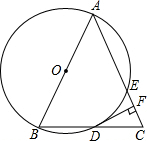
��֪���ڡ�ABC�У�AB=AC����A=36�㣬AB����O��G��H���㣬AC����O��F��E���㣬GH=FE��BH=CE��
��1����ͼ1����֤��AO��ֱƽ��BC��
��2����ͼ2��BF��CG���ڵ�M������AM�����ӳ��ֱ�GF��BC�ڵ�N��D����BH=1��GH=3��GA=2����
��ֵ��
��3����ͼ3�У�����O��ױ�BC�������е�D����G��F�ֱ�ΪAB��AC���е㣬�����ҳ���EF��ȵ��߶Σ�������֤����

��1����ͼ1����֤��AO��ֱƽ��BC��
��2����ͼ2��BF��CG���ڵ�M������AM�����ӳ��ֱ�GF��BC�ڵ�N��D����BH=1��GH=3��GA=2����
| MN |
| MD |
��3����ͼ3�У�����O��ױ�BC�������е�D����G��F�ֱ�ΪAB��AC���е㣬�����ҳ���EF��ȵ��߶Σ�������֤����

��1��֤������OP��EF��P��OQ��GH��Q����1�֣�
��EF=GH��2�֣�
��OP=OQ
��OAƽ�֡�BAC��3�֣�
��AB=AC
��AO��ֱƽ��BC����4�֣�
��2����AB=AC��BH=CE��HG=EF
��AG=AF��5�֣�
��
=
��GF��BC��6�֣�
��
=
=
=
=
=
��
��3��EF=ED=DH=HG=GF=BD=DC����7�֣����˴������һ��Ϊͬһ���÷ֵ㣩
֤������G��FΪAB��AC���е㣬D��BC���е㣬��8�֣�
��GF=
BC=BD=DC
����DF����9�֣�
��DF��AB
���1=��A=36�㣬��CDF=��B=72��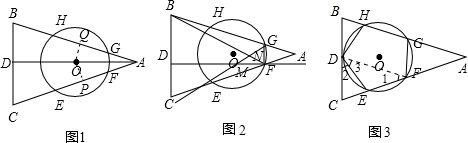
��BC��O��D
���1=��2=36�㣨10�֣�
���3=36�㣬��DEC=��C=72�㣨11�֣�
��DC=DE=EF
ͬ����HG=DH=BD����HG=EF
��EF=ED=DH=HG=GF=BD=DC��
��EF=GH��2�֣�
��OP=OQ
��OAƽ�֡�BAC��3�֣�
��AB=AC
��AO��ֱƽ��BC����4�֣�
��2����AB=AC��BH=CE��HG=EF
��AG=AF��5�֣�
��
| AG |
| AB |
| AF |
| AC |
��GF��BC��6�֣�
��
| MN |
| MD |
| GM |
| MC |
| GF |
| BC |
| AG |
| AB |
| 2 |
| 1+3+2 |
| 1 |
| 3 |
��3��EF=ED=DH=HG=GF=BD=DC����7�֣����˴������һ��Ϊͬһ���÷ֵ㣩
֤������G��FΪAB��AC���е㣬D��BC���е㣬��8�֣�
��GF=
| 1 |
| 2 |
����DF����9�֣�
��DF��AB
���1=��A=36�㣬��CDF=��B=72��

��BC��O��D
���1=��2=36�㣨10�֣�
���3=36�㣬��DEC=��C=72�㣨11�֣�
��DC=DE=EF
ͬ����HG=DH=BD����HG=EF
��EF=ED=DH=HG=GF=BD=DC��

��ϰ��ϵ�д�
�����Ŀ