题目内容
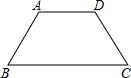
已知，如图，AB是⊙O的直径，直线EF切⊙O于点B，C和D是⊙O上的点，且∠CBE=40°，AD=CD，则∠BCD的度数是（ ）
| A．110° | B．115° | C．120° | D．130° |
如图，连接AC，
∵直线EF切⊙O于点B，
∴∠CAB=∠CBE=40°，
∵AB是⊙O的直径，
∴∠ACB=90°，
∴∠CBA=50°；
∵AD=CD，
∴∠DAC=∠DCA，
∴∠D=180°-∠CBA=130°，
∴∠DCA=
=25°，
∴∠BCD=90°+25°=115°．
故选B．
∵直线EF切⊙O于点B，
∴∠CAB=∠CBE=40°，
∵AB是⊙O的直径，
∴∠ACB=90°，
∴∠CBA=50°；
∵AD=CD，
∴∠DAC=∠DCA，
∴∠D=180°-∠CBA=130°，
∴∠DCA=
| 180°-130° |
| 2 |
∴∠BCD=90°+25°=115°．
故选B．
练习册系列答案
备战中考寒假系列答案
相关题目
