题目内容
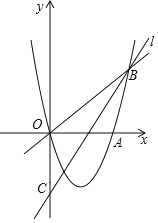
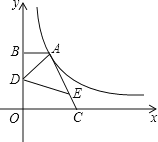
【题目】如图,点A在双曲线y=![]() 的第一象限的那一支上,AB⊥y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为
的第一象限的那一支上,AB⊥y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为![]() ,则k的值为______.
,则k的值为______.
【答案】![]()
【解析】
如下图,连接CD,由AE=3EC,△ADE的面积为![]() ,得到△CDE的面积为
,得到△CDE的面积为![]() ,则△ADC的面积为2,设A点坐标为(a,b),则k=ab,AB=a,OC=2AB=2a,BD=OD=
,则△ADC的面积为2,设A点坐标为(a,b),则k=ab,AB=a,OC=2AB=2a,BD=OD=![]() b,利用S梯形OBAC=S△ABD+S△ADC+S△ODC即可得出ab的值进而得出结论.
b,利用S梯形OBAC=S△ABD+S△ADC+S△ODC即可得出ab的值进而得出结论.
如下图,连CD
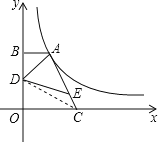
∵AE=3EC,△ADE的面积为![]() ,
,
∴△CDE的面积为![]() ,
,
∴△ADC的面积为2,
设A点坐标为(a,b),则AB=a,OC=2AB=2a,
∵点D为OB的中点,
∴BD=OD=![]() b,
b,
∵S梯形OBAC=S△ABD+S△ADC+S△ODC,
∴![]() (a+2a)×b=
(a+2a)×b=![]() a×
a×![]() b+2+
b+2+![]() ×2a×
×2a×![]() b,
b,
∴ab=![]() ,
,
把A(a,b)代入双曲线y=![]() 得,
得,
∴k=ab=![]() .
.
故答案为:![]() .
.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目