题目内容
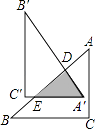
【题目】如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)直接用含t的代数式分别表示:QB= ,PD= .
(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;
(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.
【答案】(1)8-2t, ![]() .(2)不存在;当点Q的速度为每秒
.(2)不存在;当点Q的速度为每秒![]() 个单位长度时,经过
个单位长度时,经过![]() 秒,四边形PDBQ是菱形.(3)线段PQ中点M所经过的路径长为2
秒,四边形PDBQ是菱形.(3)线段PQ中点M所经过的路径长为2![]() 单位长度.
单位长度.
【解析】试题分析:(1)根据题意得:CQ=2t,PA=t,由Rt△ABC中,∠C=90°,AC=6,BC=8,PD∥BC,即可得tanA=![]() ,则可求得QB与PD的值;
,则可求得QB与PD的值;
(2)易得△APD∽△ACB,即可求得AD与BD的长,由BQ∥DP,可得当BQ=DP时,四边形PDBQ是平行四边形,即可求得此时DP与BD的长,由DP≠BD,可判定PDBQ不能为菱形;然后设点Q的速度为每秒v个单位长度,由要使四边形PDBQ为菱形,则PD=BD=BQ,列方程即可求得答案;
(3)设E是AC的中点,连接ME.当t=4时,点Q与点B重合,运动停止.设此时PQ的中点为F,连接EF,由△PMN∽△PQC.利用相似三角形的对应边成比例,即可求得答案.
试题解析:(1)根据题意得:CQ=2t,PA=t,
∴QB=8-2t,
∵在Rt△ABC中,∠C=90°,AC=6,BC=8,PD∥BC,
∴∠APD=90°,
∴tanA=![]() ,
,
∴PD= ![]() .
.
(2)不存在
在Rt△ABC中,∠C=90°,AC=6,BC=8,
∴AB=10
∵PD∥BC,
∴△APD∽△ACB,
∴![]() ,即
,即![]() ,
,
∴AD= ![]() ,
,
∴BD=AB-AD=10- ![]() ,
,
∵BQ∥DP,
∴当BQ=DP时,四边形PDBQ是平行四边形,
即8-2t= ![]() ,解得:t=
,解得:t=![]() .
.
当t=![]() 时,PD=
时,PD=![]() ,BD=10-
,BD=10-![]() ,
,
∴DP≠BD,
∴PDBQ不能为菱形.
设点Q的速度为每秒v个单位长度,
则BQ=8-vt,PD= ![]() ,BD=10-
,BD=10- ![]() ,
,
要使四边形PDBQ为菱形,则PD=BD=BQ,
当PD=BD时,即![]() =10-
=10- ![]() ,解得:t=
,解得:t=![]()
当PD=BQ,t=![]() 时,即
时,即![]() ,解得:v=
,解得:v=![]()
当点Q的速度为每秒![]() 个单位长度时,经过
个单位长度时,经过![]() 秒,四边形PDBQ是菱形.
秒,四边形PDBQ是菱形.

(3)如图2,以C为原点,以AC所在的直线为x轴,建立平面直角坐标系.
依题意,可知0≤t≤4,当t=0时,点M1的坐标为(3,0),当t=4时点M2的坐标为(1,4).
设直线M1M2的解析式为y=kx+b,
∴![]() ,
,
解得
![]() ,
,
∴直线M1M2的解析式为y=-2x+6.
∵点Q(0,2t),P(6-t,0)
∴在运动过程中,线段PQ中点M3的坐标(![]() ,t).
,t).
把x=![]() 代入y=-2x+6得y=-2×
代入y=-2x+6得y=-2×![]() +6=t,
+6=t,
∴点M3在直线M1M2上.
过点M2作M2N⊥x轴于点N,则M2N=4,M1N=2.
∴M1M2=2![]()
∴线段PQ中点M所经过的路径长为2![]() 单位长度.
单位长度.

 走进文言文系列答案
走进文言文系列答案