题目内容
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() 直线
直线![]() 经过点
经过点![]() .
.
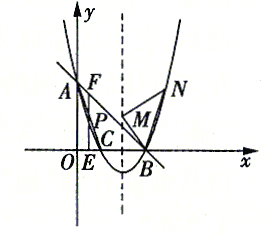
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 下方的抛物线上一动点,过点
下方的抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() 交直线
交直线![]() 于点
于点![]() 设点
设点![]() 的横坐标为
的横坐标为![]() 若
若![]() 求
求![]() 的值;
的值;
(3)![]() 是第一象限对称轴右侧抛物线上的一点,连接
是第一象限对称轴右侧抛物线上的一点,连接![]() 抛物线的对称轴上是否存在点
抛物线的对称轴上是否存在点![]() .使得
.使得![]() 与
与![]() 相似,且
相似,且![]() 为直角,若存在,请直接写出点
为直角,若存在,请直接写出点![]() 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2) ![]() 或
或![]() ;(3)存在,点
;(3)存在,点![]() 坐标为
坐标为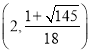 或
或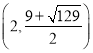
【解析】
(1)先求出点A、B坐标,用待定系数法即求出抛物线解析式;
(2)根据抛物线解析式与直线解析式表示出点P、F的坐标,然后表示出PE、PF,再列出绝对值方程,然后求解即可;
(3)先求出点C的坐标,也就求出OC的长,再设对称轴与![]() 轴交于点
轴交于点![]() 过
过![]() 点作
点作![]() 交对称轴于点
交对称轴于点![]() .根据相似三角形的性质得到KM和MQ的长,进而表示出点N的坐标,最后将点N的坐标代入函数解析式求解即可.
.根据相似三角形的性质得到KM和MQ的长,进而表示出点N的坐标,最后将点N的坐标代入函数解析式求解即可.
![]() 经过点
经过点![]() 分别在
分别在![]() 轴与
轴与![]() 轴上,
轴上,
![]() .
.
![]() 抛物线
抛物线![]() 经过点
经过点![]() ,
,
![]() ,解得
,解得![]()
![]() 抛物线的解析式为
抛物线的解析式为![]() .
.
![]() 点
点![]() 的横坐标为
的横坐标为![]()
![]() 由题意可知,点
由题意可知,点![]() 的坐标为
的坐标为![]() 点
点![]() 的坐标为
的坐标为![]() .
.
![]() 当点
当点![]() 在
在![]() 轴上方时,
轴上方时,
![]()
解得![]() 或
或![]() (与点
(与点![]() 重合,舍去).
重合,舍去).
![]()
![]() 当点
当点![]() 在
在![]() 轴下方时,
轴下方时,
![]()
解得![]() 或
或![]() (与点
(与点![]() 重合,舍去).
重合,舍去).
![]()
综上所述,![]() 的值为
的值为![]() 或
或![]()
![]() 存在,点
存在,点![]() 坐标为
坐标为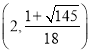 或
或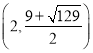
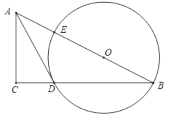
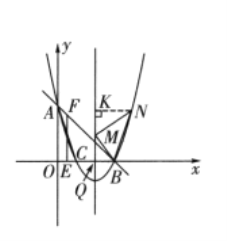
如图,设对称轴与![]() 轴交于点
轴交于点![]() 过
过![]() 点作
点作![]() 交对称轴于点
交对称轴于点![]() .
.
![]() 与
与![]() 轴交于
轴交于![]() 两点,
两点,
![]()
![]()
![]() 抛物线的对称轴为直线
抛物线的对称轴为直线![]()
![]() 当
当![]() 时,
时,![]()
由一线三垂直模型得出,
![]() .
.
![]()
![]() 设
设![]()
则![]()
![]()
![]()
![]() 点
点![]() 在抛物线上,
在抛物线上,
![]()
解得![]() (舍).
(舍).
![]() 点
点![]() 的坐标为
的坐标为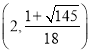
![]() 当
当![]() 时,
时,![]()
同理![]()
![]()
![]() ,
,
设![]()
则![]()
![]()
![]() 即
即![]()
![]() 点
点![]() 在抛物线上,
在抛物线上,
![]()
解得![]() (舍),
(舍),
![]() 点
点![]() 的坐标为
的坐标为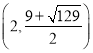
综上所述,存在点![]() 点
点![]() 的坐标为
的坐标为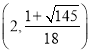 ,
,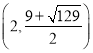

 智慧小复习系列答案
智慧小复习系列答案【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下尚不完整的统计图表.
调查结果统计表
组别 | 分组(单位:元) | 人数 |
A |
|
|
B |
|
|
C |
|
|
D |
|
|
E |
|
|
调查结果扇形统计图
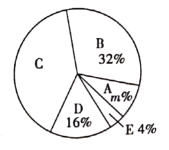
请根据以上图表,解答下列问题:
(1)这次被调查的同学共有______人,![]() ______,
______,![]() _______;
_______;
(2求扇形统计图中C所在的扇形的圆心角度数;.
(3)该校共有学生![]() 人,请估计每月零花钱的数额
人,请估计每月零花钱的数额![]() 在
在![]() 范围内的人数.
范围内的人数.