Question

【题目】已知抛物线经过定点A．

（1）直接写出A点坐标；

（2）直线y=t (t<6)与抛物线交于B，C两点（B在C 的左边），过点A作AD⊥BC于点D，是否存在t的值，使得对于任意的m，∠DAC=∠ABD恒成立，若存在，请求t的值；若不存在，请说明理由．

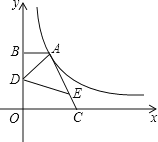
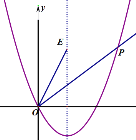
（3）如图，当m=1时，直线y=2x交对称轴于点E，在直线OE的右侧作∠EOP交抛物线于点P，使得tan∠EOP=，已知x轴上有一个点M(t，0)， EM+PM是否存在最小值？若存在，求t的值；若不存在，请说明理由．

Answer 1

【答案】(1)A(-2，6)；(2)存在，；(3)存在，

【解析】

(1)将解析式变形，得到m的系数为0，即可得出点A的坐标；

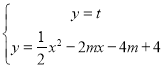(2)设B、C的横坐标分别为，由方程组得：，得到，，根据题意证得△ADC∽△BDA，得，即，即可求得答案；

(3)先求得点E的坐标，利用tan∠EOP=，求得，从而依次求得点G的坐标为(，)、直线OP的解析式、点P的坐标，点E关于轴的对称点F，利用轴对称的性质找到点M，求得直线FP的解析式即可求解．

(1)∵抛物线，

∴当时，无论为何值，抛物线经过定点A，
∴，，
∴定点A的坐标为(，)；
(2)设直线与抛物线的交点B、C两点的横坐标分别为，

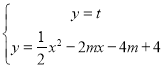由方程组得：，

∴，，

∵∠DAC=∠ABD，∠ADC=∠BDA，

∴△ADC∽△BDA，

∴，

∴，

∵，，，

∴，

整理得：，

解得：(舍去)，

∴当t时，使得对于任意的m，∠DAC=∠ABD恒成立；

(3)当时，抛物线的解析式为，对称轴为直线，

设对称轴交OP于G，交轴于H，如图：

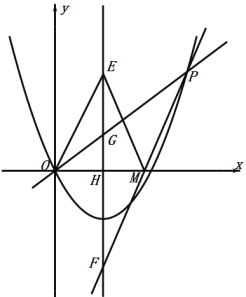
∵直线交对称轴于点E，

∴点E的坐标为(，)，

∴OH=2，EH=4，

，

∵，

∴，

∴，

设GH=，则，

∵，即，

解得：，

∴点G的坐标为(，)，

设直线OP的解析式为：，

把点G的坐标为(，)代入得：，

∴直线OP的解析式为：，

解方程组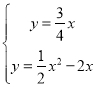得：或，

∴点P的坐标为(，)，

作点E关于轴的对称点F，连接PF交轴于点M，此时EM+PM取得最小值，

∵点E的坐标为(，)，

∴点F的坐标为(，)，

设直线FP的解析式为：，

把点F、点P的坐标代入得：，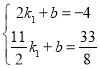

解得：，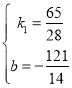

∴直线FP的解析式为：，

令，则，

∴点M的坐标为(，)，

∴当时，EM+PM存在最小值．