Question

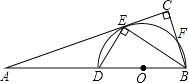
【题目】如图，在菱形ABCD中，对角线AC与BD相交于点O，过点D作DE⊥BD交BC的延长线于点E.

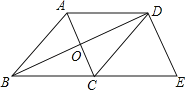
（1）求证：四边形ACED是平行四边形；

（2）若BD＝4，AC＝3，求cos∠CDE的值.

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）想办法证明AC∥DE，AD∥CE即可；

（2）只要证明∠CDE＝∠E，再想办法求出cos∠E即可；

（1）证明：∵四边形ABCD是菱形

∴AD∥BC，∠BOC＝90°，

∵DE⊥BD，

∴∠BDE＝90°，

∴∠BDE＝∠BOC，

∴AC∥DE，

∴四边形ACED是平行四边形.

（2）解：∵四边形ACED是平行四边形，

∴AD＝CE，

∵AD＝BC，

∴BC＝CE，

∵∠BDE＝90°，

∴DC＝CE，

∴∠CDE＝∠E

∴cos∠CDE＝cos∠E，

∵BD＝4，AC＝3，∠BDE＝90°，

∴BE＝5，

∴cos∠E＝＝，

∴cos∠CDE＝cos∠E＝.