题目内容
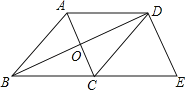
【题目】已知:如图,BD是半圆O的直径,A是BD延长线上的一点,BC⊥AE,交AE的延长线于点C,交半圆O于点E,且E为![]() 的中点.
的中点.
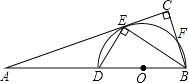
(1)求证:AC是半圆O的切线;
(2)若AD=6,AE=6![]() ,求BC的长.
,求BC的长.
【答案】(1)可证明∠AEO=∠C=90°.即DE⊥AC.又OE为半圆O的半径,
∴AC是半圆O的切线.(2)BC=4.
【解析】
试题解:(1)连接OE。
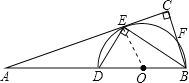
∵E为![]() 的中点,
的中点,
∴![]() =
=![]() .
.
∴∠OBE=∠CBE.
∵OE=OB,
∴∠OEB=∠OBE.
∴∠OEB=∠CBE.
∴OE∥BC.
∵BC⊥AC,∴∠C=90°.
∴∠AEO=∠C=90°.即DE⊥AC.
又OE为半圆O的半径,
∴AC是半圆O的切线.
(2)设⊙O的半径为x
∵OE⊥AC,
∴(x+6)2-(6![]() )2=x2.
)2=x2.
∴x=3.
∴AB=AD+OD+OB=12.
∵OE∥BC,
∴△AOE~△ABC.
∴![]() =
=![]()
即![]() =
=![]()
∴BC=4.。

【题目】同学们设计了一个重复抛掷的实验:全班48人分为8个小组,每组抛掷同一型号的一枚瓶盖300次,并记录盖面朝上的次数,下表是依次累计各小组的实验结果.
1组 | 1~2组 | 1~3组 | 1~4组 | 1~5组 | 1~6组 | 1~7组 | 1~8组 | |
盖面朝上次数 | 165 | 335 | 483 | 632 | 801 | 949 | 1122 | 1276 |
盖面朝上频率 | 0.550 | 0.558 | 0.537 | 0.527 | 0.534 | 0.527 | 0.534 | 0.532 |
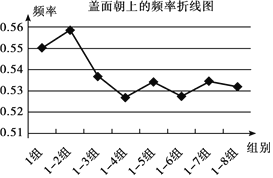
根据实验,你认为这一型号的瓶盖盖面朝上的概率为____,理由是:____.
【题目】每个人都应怀有对水的敬畏之心,从点滴做起,节水、爱水,保护我们生活的美好世界.某地近年来持续干旱,为倡导节约用水,该地采用了“阶梯水价”计费方法,具体方法:每户每月用水量不超过4吨的每吨2元;超过4吨而不超过6吨的,超出4吨的部分每吨4元;超过6吨的,超出6吨的部分每吨6元.该地一家庭记录了去年12个月的月用水量如下表,下列关于用水量的统计量不会发生改变的是( )
用水量x(吨) | 3 | 4 | 5 | 6 | 7 |
频数 | 1 | 2 | 5 | 4﹣x | x |
A. 平均数、中位数 B. 众数、中位数 C. 平均数、方差 D. 众数、方差