Question

【题目】如图1，分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC，EG剪开，拼成如图2所示的ALMN，若中间空白部分四边形OPQR恰好是正方形，且ALMN的面积为50，则正方形EFGH的面积为（　　）

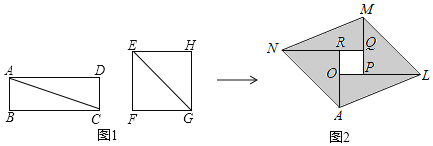
A. 24 B. 25 C. 26 D. 27

Answer 1

【答案】B

【解析】

此题涉及的知识点是正方形、长方形的性质，先根据正方形和长方形的性质求出各边长的关系，再根据ALMN的面积，求出各边长的关系，最后得出面积.

设EF=a，BC=b，AB=c，则PQ=a-c，RQ=b-a，PQ=RQ

∴a=，

∵ALMN的面积为50，∴bc+a2+(a-c)2=50,

把a=代入化简求值得b+c=10, ∴a=5,

∴正方形EFGH的边长为5，

∴正方形EFGH的面积为25，

故选B.