题目内容
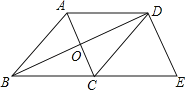
【题目】已知,在Rt△ABC中,∠B=90°,AB=![]() ,BC=3,在BC边上取两点E,F(点E在点F左侧),以EF为边作等边三角形DEF,使顶点D与E在边AC异侧,DE,DF分别交AC于点G,H,连结AD.
,BC=3,在BC边上取两点E,F(点E在点F左侧),以EF为边作等边三角形DEF,使顶点D与E在边AC异侧,DE,DF分别交AC于点G,H,连结AD.

(1)如图1,求证:DE⊥AC;
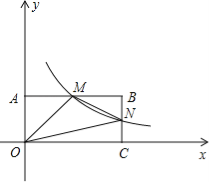
(2)如图2,若∠DAC=30°,△DEF的边EF在线段BC上移动.写出DH与BE的数量关系并证明;
(3)若30°<∠DAC<60°,△DEF的周长为m,则m的取值范围是 .
【答案】(1)见解析;(2)DH与BE的数量关系是:DH﹣BE=1,理由见解析;(3)6<m<9
【解析】
(1)先判断出∠C=30°,再利用等边三角形的性质即可得出结论;
(2)先判断出AD∥BC,进而判断出四边形ABEN是矩形,再用锐角三角函数求出ND=1,即可得出结论;
(3)先求出∠DAC=30°和60°时的等边三角形的边DE的长,即可得出结论.
解:(1)在Rt△ABC中,∵∠B=90°,AB=![]() ,BC=3,
,BC=3,
∴tan∠C=![]()
∴∠C=30°
∵△DEF是等边三角形
∴∠DEF=60°
∴∠EGC=90°
∴DE⊥AC
(2)DH与BE的数量关系是:DH﹣BE=1
理由:如图1,∵△DEF是等边三角形

∴∠DFE=∠DEF=60°
∵∠DFE=∠C+∠CHF,∠C=30°
∴∠CHF=30°
∴∠DHA=30°
∵∠DAC=30°
∴∠DHA=∠DAC
∴DA=DH
过点E作EN⊥AD于N,则∠ANE=90°,
∵∠DAC=∠C=30°
∴AD‖BC
∴∠BEN=90
又∵∠B=90°
∴四边形ABEN是矩形
∴AN=BE,AB=EN=![]()
∵AD‖BC
∴∠DEF=∠NDE=60°
∴tan∠NDE═tan60°=![]()
∴ND=1
∵AD﹣AN=ND,DA=DH,AN=BE
∴DH﹣BE=1,
(3)当∠DAC=30°时,平移DE,使其过点B时,如图2,
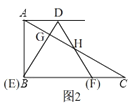
∵∠BAC=60°,
∴∠BAD=90°,
∵∠ABC=90°,
∵△DEF是等边三角形,
∴∠DBC=60°,
∵∠ABC=90°,
∴∠ABD=30°,
在Rt△ABD中,AB=![]() ,∠ABD=30°,
,∠ABD=30°,
∴DE=DB=2,
由于∠ABD不变,∠DAC增加时,∠BAD增加,即:DE增加,
∵∠DAC>30°,
∴DE>2,
∴m>2×3,
即:m>6,
当∠DAC=60°时,平移DE,使其过点B时,如图3,

∵∠BAC=60°,
∴∠BAD=120°,
∵△DEF是等边三角形,
∴∠DBC=60°,
∵∠ABC=90°,
∴∠ABD=30°,
∴∠ADB=30°=∠ABD,
∴AC⊥BD,BD=2BG,
在Rt△ABG中,AB=![]() ,∠ABD=30°,
,∠ABD=30°,
∴BG=![]() ,
,
∴DE=BD=2BG=3,
∵BC=3,
此时点F和点C重合,
由于∠ABD不变,∠DAC减小时,∠BAD减小,即:DE减小,
∵∠CAD<60°,
∴DE<3,
∴m<3×3,
∴m<9,
即:m的取值范围是:6<m<9,
故答案为:6<m<9.

 阅读快车系列答案
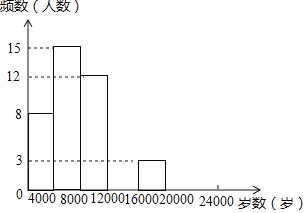
阅读快车系列答案【题目】现今“微信运动”被越来越多的人关注和喜爱,某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理,绘制了如下的统计图表(不完整):
步数 | 频数 | 频率 |
0≤x<4000 | 8 | a |
4000≤x<8000 | 15 | 0.3 |
8000≤x<12000 | 12 | b |
12000≤x<16000 | c | 0.2 |
16000≤x<20000 | 3 | 0.06 |
20000≤x<24000 | d | 0.04 |
请根据以上信息,解答下列问题:
(1)写出a,b,c,d的值并补全频数分布直方图;
(2)本市约有37800名教师,用调查的样本数据估计日行走步数超过12000步(包含12000步)的教师有多少名?
(3)若在50名被调查的教师中,选取日行走步数超过16000步(包含16000步的两名教师与大家分享心得,求被选取的两名教师恰好都在20000步(包含20000步)以上的概率.
【题目】同学们设计了一个重复抛掷的实验:全班48人分为8个小组,每组抛掷同一型号的一枚瓶盖300次,并记录盖面朝上的次数,下表是依次累计各小组的实验结果.
1组 | 1~2组 | 1~3组 | 1~4组 | 1~5组 | 1~6组 | 1~7组 | 1~8组 | |
盖面朝上次数 | 165 | 335 | 483 | 632 | 801 | 949 | 1122 | 1276 |
盖面朝上频率 | 0.550 | 0.558 | 0.537 | 0.527 | 0.534 | 0.527 | 0.534 | 0.532 |
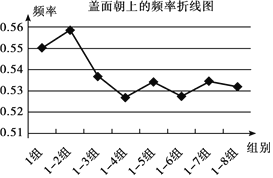
根据实验,你认为这一型号的瓶盖盖面朝上的概率为____,理由是:____.