ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ“―÷Σ![]() «
«![]() ΒΡΚ· ΐΘ§Ή‘±δΝΩ
ΒΡΚ· ΐΘ§Ή‘±δΝΩ![]() ΒΡ»Γ÷ΒΖΕΈß «
ΒΡ»Γ÷ΒΖΕΈß «![]() ΒΡ»ΪΧε Β ΐΘ§»γ±μ «
ΒΡ»ΪΧε Β ΐΘ§»γ±μ «![]() ”κ
”κ![]() ΒΡΦΗΉιΕ‘”Π÷ΒΘ°
ΒΡΦΗΉιΕ‘”Π÷ΒΘ°

–ΓΜΣΗυΨί―ßœΑΚ· ΐΒΡΨ≠―ιΘ§άϊ”Ο…œ ω±μΗώΥυΖ¥”≥≥ωΒΡ![]() ”κ
”κ![]() ÷°ΦδΒΡ±δΜ·Ιφ¬…Θ§Ε‘ΗΟΚ· ΐΒΡΆΦœσ”κ–‘÷ Ϋχ––ΝΥΧΫΨΩΘ°œ¬Οφ «–ΓΜΣΒΡΧΫΨΩΙΐ≥ΧΘ§«κ≤Ι≥δΆξ’ϊΘΚ
÷°ΦδΒΡ±δΜ·Ιφ¬…Θ§Ε‘ΗΟΚ· ΐΒΡΆΦœσ”κ–‘÷ Ϋχ––ΝΥΧΫΨΩΘ°œ¬Οφ «–ΓΜΣΒΡΧΫΨΩΙΐ≥ΧΘ§«κ≤Ι≥δΆξ’ϊΘΚ
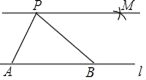
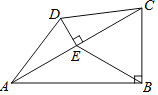
Θ®1Θ©¥”±μΗώ÷–ΕΝ≥ωΘ§Β±Ή‘±δΝΩ «©¹2 ±Θ§Κ· ΐ÷Β «ΓΓ ΓΓΘΜ
Θ®2Θ©»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§Οη≥ωΝΥ“‘…œ±μ÷–ΗςΕ‘Ε‘”Π÷ΒΈΣΉχ±ξΒΡΒψΘ°ΗυΨίΟη≥ωΒΡΒψΘ§Μ≠≥ωΗΟΚ· ΐΒΡΆΦœσΘΜ
÷–Θ§Οη≥ωΝΥ“‘…œ±μ÷–ΗςΕ‘Ε‘”Π÷ΒΈΣΉχ±ξΒΡΒψΘ°ΗυΨίΟη≥ωΒΡΒψΘ§Μ≠≥ωΗΟΚ· ΐΒΡΆΦœσΘΜ
Θ®3Θ©‘ΎΜ≠≥ωΒΡΚ· ΐΆΦœσ…œ±ξ≥ω![]() ±ΥυΕ‘”ΠΒΡΒψΘ§≤Δ–¥≥ω
±ΥυΕ‘”ΠΒΡΒψΘ§≤Δ–¥≥ω![]() ΓΓ ΓΓΘ°
ΓΓ ΓΓΘ°
Θ®4Θ©ΫαΚœΚ· ΐΒΡΆΦœσΘ§–¥≥ωΗΟΚ· ΐΒΡ“ΜΧθ–‘÷ ΘΚΓΓ ΓΓΘ°
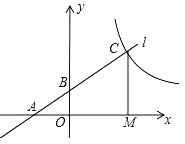
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©ΦϊΫβΈωΘΜΘ®3Θ©
ΘΜΘ®2Θ©ΦϊΫβΈωΘΜΘ®3Θ©![]() ΘΜΘ®4Θ©Β±
ΘΜΘ®4Θ©Β±![]() ±Θ§
±Θ§![]() Υφ
Υφ![]() ΒΡ‘ω¥σΕχΦθ–ΓΘ°
ΒΡ‘ω¥σΕχΦθ–ΓΘ°
ΓΨΫβΈωΓΩ
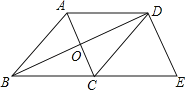
Θ®1Θ©ΗυΨί±μ÷–![]() Θ§
Θ§![]() ΒΡΕ‘”Π÷ΒΦ¥Ω…ΒΟΒΫΫα¬έΘΜ
ΒΡΕ‘”Π÷ΒΦ¥Ω…ΒΟΒΫΫα¬έΘΜ
Θ®2Θ©Α¥’’Ή‘±δΝΩ”…–ΓΒΫ¥σΘ§άϊ”ΟΤΫΜ§ΒΡ«ζœΏΝ§ΫαΗςΒψΦ¥Ω…ΘΜ
Θ®3Θ©‘ΎΥυΜ≠ΒΡΚ· ΐΆΦœσ…œ’“≥ωΉ‘±δΝΩΈΣ7ΥυΕ‘”ΠΒΡΚ· ΐ÷ΒΦ¥Ω…ΘΜ
Θ®4Θ©άϊ”ΟΚ· ΐΆΦœσΒΡΆΦœσ«σΫβΘ°
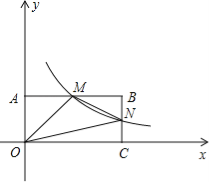
ΫβΘΚΘ®1Θ©Β±Ή‘±δΝΩ «©¹2 ±Θ§Κ· ΐ÷Β «![]() ΘΜ
ΘΜ
Ι ¥πΑΗΈΣΘΚ![]() .
.
Θ®2Θ©ΗΟΚ· ΐΒΡΆΦœσ»γΆΦΥυ ΨΘΜ
Θ®3Θ©Β±![]() ±ΥυΕ‘”ΠΒΡΒψ »γΆΦΥυ ΨΘ§
±ΥυΕ‘”ΠΒΡΒψ »γΆΦΥυ ΨΘ§
«“![]() ΘΜ
ΘΜ
Ι ¥πΑΗΈΣΘΚ![]() ΘΜ
ΘΜ
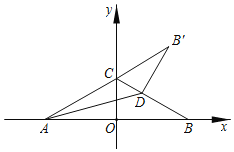
Θ®4Θ©Κ· ΐΒΡ–‘÷ ΘΚΒ±![]() ±Θ§
±Θ§![]() Υφ
Υφ![]() ΒΡ‘ω¥σΕχΦθ–ΓΘ°
ΒΡ‘ω¥σΕχΦθ–ΓΘ°
Ι ¥πΑΗΈΣΘΚΒ±![]() ±Θ§
±Θ§![]() Υφ
Υφ![]() ΒΡ‘ω¥σΕχΦθ–ΓΘ°
ΒΡ‘ω¥σΕχΦθ–ΓΘ°

ΓΨΧβΡΩΓΩΆ§―ßΟ«…ηΦΤΝΥ“ΜΗω÷ΊΗ¥≈Ή÷άΒΡ Β―ιΘΚ»ΪΑύ48»ΥΖ÷ΈΣ8Ηω–ΓΉιΘ§ΟΩΉι≈Ή÷άΆ§“Μ–ΆΚ≈ΒΡ“ΜΟΕΤΩΗ«300¥ΈΘ§≤ΔΦ«¬ΦΗ«Οφ≥·…œΒΡ¥Έ ΐΘ§œ¬±μ «“ά¥ΈάέΦΤΗς–ΓΉιΒΡ Β―ιΫαΙϊ.
1Ήι | 1ΓΪ2Ήι | 1ΓΪ3Ήι | 1ΓΪ4Ήι | 1ΓΪ5Ήι | 1ΓΪ6Ήι | 1ΓΪ7Ήι | 1ΓΪ8Ήι | |
Η«Οφ≥·…œ¥Έ ΐ | 165 | 335 | 483 | 632 | 801 | 949 | 1122 | 1276 |
Η«Οφ≥·…œΤΒ¬ | 0.550 | 0.558 | 0.537 | 0.527 | 0.534 | 0.527 | 0.534 | 0.532 |
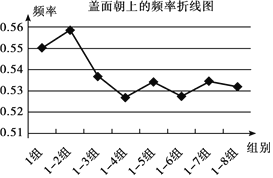
ΗυΨί Β―ιΘ§Ρψ»œΈΣ’β“Μ–ΆΚ≈ΒΡΤΩΗ«Η«Οφ≥·…œΒΡΗ≈¬ ΈΣ____Θ§άμ”… «ΘΚ____.
ΓΨΧβΡΩΓΩΟΩΗω»ΥΕΦ”ΠΜ≥”–Ε‘Υ°ΒΡΨ¥ΈΖ÷°–ΡΘ§¥”ΒψΒΈΉωΤπΘ§ΫΎΥ°ΓΔΑ°Υ°Θ§±ΘΜΛΈ“Ο«…ζΜνΒΡΟάΚΟ άΫγΘ°Ρ≥ΒΊΫϋΡξά¥≥÷–χΗ…ΚΒΘ§ΈΣ≥ΪΒΦΫΎ‘Φ”ΟΥ°Θ§ΗΟΒΊ≤…”ΟΝΥΓΑΫΉΧίΥ°ΦέΓ±ΦΤΖ―ΖΫΖ®Θ§ΨΏΧεΖΫΖ®ΘΚΟΩΜßΟΩ‘¬”ΟΥ°ΝΩ≤Μ≥§Ιΐ4Ε÷ΒΡΟΩΕ÷2‘ΣΘΜ≥§Ιΐ4Ε÷Εχ≤Μ≥§Ιΐ6Ε÷ΒΡΘ§≥§≥ω4Ε÷ΒΡ≤ΩΖ÷ΟΩΕ÷4‘ΣΘΜ≥§Ιΐ6Ε÷ΒΡΘ§≥§≥ω6Ε÷ΒΡ≤ΩΖ÷ΟΩΕ÷6‘ΣΘ°ΗΟΒΊ“ΜΦ“ΆΞΦ«¬ΦΝΥ»ΞΡξ12Ηω‘¬ΒΡ‘¬”ΟΥ°ΝΩ»γœ¬±μΘ§œ¬Ν–ΙΊ”Ύ”ΟΥ°ΝΩΒΡΆ≥ΦΤΝΩ≤ΜΜαΖΔ…ζΗΡ±δΒΡ «Θ®ΓΓΓΓΘ©
”ΟΥ°ΝΩxΘ®Ε÷Θ© | 3 | 4 | 5 | 6 | 7 |
ΤΒ ΐ | 1 | 2 | 5 | 4©¹x | x |
A. ΤΫΨυ ΐΓΔ÷–ΈΜ ΐ B. ÷Ύ ΐΓΔ÷–ΈΜ ΐ C. ΤΫΨυ ΐΓΔΖΫ≤ν D. ÷Ύ ΐΓΔΖΫ≤ν