Question

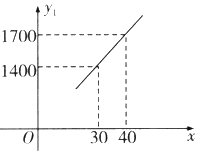
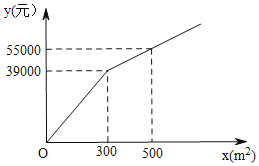
【题目】我国为了实现到2020年达到全面小康社会的目标，近几年加大了扶贫工作的力度，合肥市某知名企业为了帮助某小型企业脱贫，投产一种书包，每个书包制造成本为18元，试销过程中发现，每月销售量y(万个)与销售单价x(元)之间的关系可以近似看作一次函数y＝kx+b，据统计当售价定为30元/个时，每月销售40万个，当售价定为35元/个时，每月销售30万个．

(1)请求出k、b的值．

(2)写出每月的利润w(万元)与销售单价x(元)之间的函数解析式．

(3)该小型企业在经营中，每月销售单价始终保持在25≤x≤36元之间，求该小型企业每月获得利润w(万元)的范围．

Answer 1

【答案】(1)k的值为﹣2，b的值为100；(2)w＝﹣2x2+136x﹣1800；(3)该小型企业每月获得利润w(万元)的范围是350≤w≤512．

【解析】

（1）待定系数法求出k和b的值即可；
（2）利用（售价-成本）乘以销售量等于利润可列式求解；
（3）根据二次函数的顶点值，及顶点左右两侧增减变化的性质来求解即可．

解：(1)由题意得： ，

解得 ．

答：k的值为﹣2，b的值为100；

(2)由题意得w＝(x﹣18)(﹣2x+100)＝﹣2x2+136x﹣1800，

答：函数解析式为：w＝﹣2x2+136x﹣1800；

(3)∵w＝﹣2x2+136x﹣1800＝﹣2(x﹣34)2+512，

∴当x＝34时，w取最大值，最大值为512；

当x＜34时，w随着x的增大而增大；

当x＞34时，w随着x的增大而减小．

∵当x＝25时，

w＝﹣2×252+136×25﹣1800＝350；

当x＝36时，

w＝﹣2×362+136×36﹣1800＝504．

综上，w的范围为350≤w≤512．

答：该小型企业每月获得利润w(万元)的范围是350≤w≤512．