题目内容
如图，若点M是x轴正半轴上任意一点，过点M作PQ∥y轴，分别交函数
和
的图象于点P和Q，连接OP和OQ．则下列结论正确的是（ ）
| A．∠POQ不可能等于90° |
B． |
| C．这两个函数的图象一定关于x轴对称 |
D．△POQ的面积是 |
D.
解析试题分析： A．∵P点坐标不知道，当PM=MQ时，并且PM=OM，∠POQ等于90°，故此选项错误；
B．根据图形可得：k1＞0，k2＜0，而PM，QM为线段一定为正值，故
，故此选项错误；
C．根据k1，k2的值不确定，得出这两个函数的图象不一定关于x轴对称，故此选项错误；
D．∵|k1|=PM•MO，|k2|=MQ•MO，△POQ的面积=
MO•PQ=MO（PM+MQ）=MO•PM+MO•MQ，
∴△POQ的面积是，故此选项正确．
故选：D．
考点：反比例函数综合题．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
已知点(－1，y1)、(2，y2)、(3，y3)在反比例函数
的图象上．下列结论中正确的是
| A．y1>y2>y3 | B．y1>y3>y2 | C．y3>y1>y2 | D．y2>y3>y1 |
如图，在平面直角坐标系中，BA⊥y轴于点A，BC⊥x轴于点C，函数
的图象分别交BA，BC于点D，E.当AD:BD=1:3且
BDE的面积为18时，则
的值是（ ）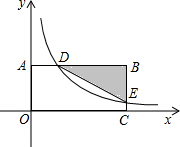
| A．9.6 | B．12 | C．14.4 | D．16 |
反比例函数y=
的图象在（ ）
| A．第一，二象限 | B．第一，三象限 |
| C．第二，四象限 | D．第三，四象限 |
如图，已知第一象限内的点A在反比例函数
上，第二象限的点B在反比例函数
上，且OA⊥OB，
，则k的值为 （ ）
| A．－3 | B．－6 | C．－4 | D． |
如图，△AOB为等边三角形，点A在第四象限，点B的坐标为（4，0），过点C（
4，0）作直线l交AO于D，交AB于E，且点E在某反比例函数
图象上，当△ADE和△DCO的面积相等时，k的值为（ ）
A． | B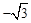． | C． | D． |
已知(x1，y1)，(x2，y2)，(x3，y3)是反比例函数
的图象上的三点，且x1＜x2＜0，x3＞0，则y1，y2，y3的大小关系是( )．
| A．y3＜y1＜y2 | B．y2＜y1＜y3 | C．y1＜y2＜y3 | D．y3＜y2＜y1 |
若反比例函数经过点（1,2），则下列点也在此函数图象上的是（ ）
| A．（1，-2） | B．（-1，﹣2） | C．（0，﹣1） | D．（﹣1，﹣1） |
当a≠0时，函数y=ax+1与函数
在同一坐标系中的图象可能是
A． | B． | C． | D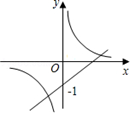． |