题目内容
如图,已知第一象限内的点A在反比例函数 上,第二象限的点B在反比例函数
上,第二象限的点B在反比例函数 上,且OA⊥OB,
上,且OA⊥OB, ,则k的值为 ( )
,则k的值为 ( )
| A.-3 | B.-6 | C.-4 | D. |
B.
解析试题解析:过A作AE⊥x轴,过B作BF⊥x轴,由OA与OB垂直,再利用邻补角定义得到一对角互余,再由直角三角形BOF中的两锐角互余,利用同角的余角相等得到一对角相等,又一对直角相等,利用两对对应角相等的三角形相似得到三角形BOF与三角形OEA相似,在直角三角形AOB中,由锐角三角函数定义,根据cos∠BAO的值,设出AB与OA,利用勾股定理表示出OB,求出OB与OA的比值,即为相似比,根据面积之比等于相似比的平方,求出两三角形面积之比,由A在反比例函数y= 上,利用反比例函数比例系数的几何意义求出三角形AOE的面积,进而确定出BOF的面积,再利用k的几何意义即可求出k的值.
上,利用反比例函数比例系数的几何意义求出三角形AOE的面积,进而确定出BOF的面积,再利用k的几何意义即可求出k的值.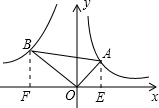
本题选B.
考点: 反比例函数.

练习册系列答案
相关题目
当x<0时,函数 的图象在( )
的图象在( )
| A.第四象限 | B.第三象限 | C.第二象限 | D.第一象限 |
如图,正方形OABC,ADEF的顶点A,D,C在坐标轴上,点F在AB上,点B,E在函数y= (x>0)的图象上,则点E的坐标是( )
(x>0)的图象上,则点E的坐标是( )
A.( +1, +1, ﹣1) ﹣1) | B.(3+ ,3﹣ ,3﹣ ) ) |
C.( ﹣1, ﹣1, +1) +1) | D.(3﹣ ,3+ ,3+ ) ) |
如图,若点M是x轴正半轴上任意一点,过点M作PQ∥y轴,分别交函数 和
和 的图象于点P和Q,连接OP和OQ.则下列结论正确的是( )
的图象于点P和Q,连接OP和OQ.则下列结论正确的是( )
| A.∠POQ不可能等于90° |
B. |
| C.这两个函数的图象一定关于x轴对称 |
D.△POQ的面积是 |
已知反比例函数y= 的图象上有两点A(x1,y1)、B(x2,y2),当x1<0<x2时,有y1<y2,则m的取值范围是
的图象上有两点A(x1,y1)、B(x2,y2),当x1<0<x2时,有y1<y2,则m的取值范围是
A.m< | B.m>0 | C.m<0 | D.m> |
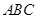 的边长为3,N为AC的三等分点,三角形边上的动点M从点A出发,沿A
的边长为3,N为AC的三等分点,三角形边上的动点M从点A出发,沿A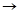 B
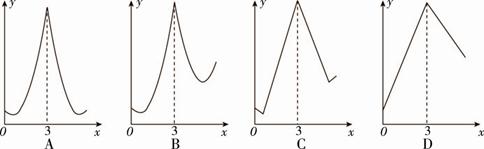
B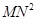 为y,则y关于x的函数图象大致为( )
为y,则y关于x的函数图象大致为( )




 的图象的一支经过矩形对角线的交点P,则该反比例函数的解析式是( )
的图象的一支经过矩形对角线的交点P,则该反比例函数的解析式是( )



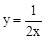
 的图象上有一点A,AB平行于x轴交y轴于点B,△ABO的面积是1,则反比例函数的解析式是
的图象上有一点A,AB平行于x轴交y轴于点B,△ABO的面积是1,则反比例函数的解析式是



