题目内容
如图,在平面直角坐标系中,BA⊥y轴于点A,BC⊥x轴于点C,函数
 的图象分别交BA,BC于点D,E.当AD:BD=1:3且
的图象分别交BA,BC于点D,E.当AD:BD=1:3且 BDE的面积为18时,则
BDE的面积为18时,则 的值是( )
的值是( )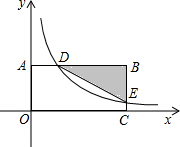
| A.9.6 | B.12 | C.14.4 | D.16 |
D.
解析试题分析:如图,过点D作DF⊥x轴于点F,过点E作EG⊥y轴于点G.
设B(4a,b),E(4a,d),
∵AD:BD=1:3,∴D(a,b).
又∵△BDE的面积为18,∴BD=3a,BE="b-d."
∴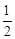 ×3a(b-d)=18,即a(b-d)=12,即ab-ad=12.
×3a(b-d)=18,即a(b-d)=12,即ab-ad=12.
∵D,E都在反比例函数图象上,∴ab="4ad." ∴4ad-ad=12,解得:ad=4.
∴k=4ad=16.
故选D.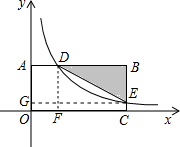
考点:反比例函数系数k的几何意义.

练习册系列答案
相关题目
若反比例函数 的图象位于第二、四象限,则k的取值可以是( )
的图象位于第二、四象限,则k的取值可以是( )
| A.0 | B.1 | C.2 | D.以上都不是 |
当x<0时,函数 的图象在( )
的图象在( )
| A.第四象限 | B.第三象限 | C.第二象限 | D.第一象限 |
已知点P(-1,4)在反比例函数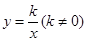 的图象上,则k的值是 ( )
的图象上,则k的值是 ( )
A.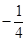 | B. | C.4 | D.-4 |
如图,若点M是x轴正半轴上任意一点,过点M作PQ∥y轴,分别交函数 和
和 的图象于点P和Q,连接OP和OQ.则下列结论正确的是( )
的图象于点P和Q,连接OP和OQ.则下列结论正确的是( )
| A.∠POQ不可能等于90° |
B. |
| C.这两个函数的图象一定关于x轴对称 |
D.△POQ的面积是 |
y=ax+b与y= 的图象,如图所示,则
的图象,如图所示,则
| A.a>0,b>0,c>0 | B.a<0,b<0,c<0 |
| C.a<0,b>0,c>0 | D.a<0,b<0,c>0 |
函数y1=x和 的图象如图所示,则y1>y2的x取值范围是
的图象如图所示,则y1>y2的x取值范围是
| A.x<﹣1或x>1 | B.x<﹣1或0<x<1 |
| C.﹣1<x<0或x>1 | D.﹣1<x<0或0<x<1 |
 上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于
上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于 轴、
轴、 轴,若双曲线
轴,若双曲线 (
( )与△ABC有交点,则
)与△ABC有交点,则 的取值范围是( )
的取值范围是( )
 B.
B. C.
C. D.
D.
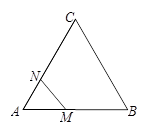
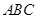 的边长为3,N为AC的三等分点,三角形边上的动点M从点A出发,沿A
的边长为3,N为AC的三等分点,三角形边上的动点M从点A出发,沿A B
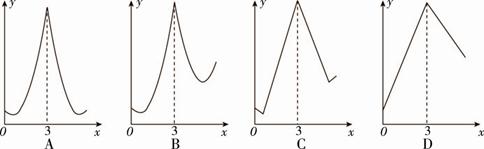
B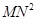 为y,则y关于x的函数图象大致为( )
为y,则y关于x的函数图象大致为( )