题目内容
如图,△AOB为等边三角形,点A在第四象限,点B的坐标为(4,0),过点C( 4,0)作直线l交AO于D,交AB于E,且点E在某反比例函数
4,0)作直线l交AO于D,交AB于E,且点E在某反比例函数 图象上,当△ADE和△DCO的面积相等时,k的值为( )
图象上,当△ADE和△DCO的面积相等时,k的值为( )
A. | B.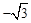 | C. | D. |
C.
解析试题分析:如图,连接AC,
∵点B的坐标为(4,0),△AOB为等边三角形,∴AO="OB=4." ∴点A的坐标为 .
.
∵C( 4,0),∴AO=OC=4,∴∠OCA=∠OAC.
4,0),∴AO=OC=4,∴∠OCA=∠OAC.
∵∠AOB=60°,∴∠ACO=30°.
又∵∠B="60°." ∴∠BAC=90°.
∵S△ADE=S△DCO,S△AEC=S△ADE+S△ADC,S△AOC=S△DCO+S△ADC,
∴S△AEC=S△AOC= ,即
,即  .
.
∴E点为AB的中点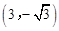 .
.
把E点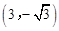 代入
代入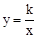 中得:k=
中得:k= .
.
故选C.
考点:1. 等边三角形的性质;2. 等腰三角形的判定和性质;3.三角形内角和定理;4.曲线上点的坐标与方程的关系.

 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案已知反比例函数y=﹣ 的图象上有两点A(x1,y1),B(x2,y2),若x1<0<x2,则下列判断正确的是()
的图象上有两点A(x1,y1),B(x2,y2),若x1<0<x2,则下列判断正确的是()
| A.y1<y2<0 | B.0<y2<y1 | C.y1<0<y2 | D.y2<0<y1 |
已知点P(-1,4)在反比例函数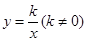 的图象上,则k的值是 ( )
的图象上,则k的值是 ( )
A.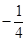 | B. | C.4 | D.-4 |
已知点P(-1,3)在反比例函数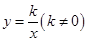 的图象上,则k的值是 ( )
的图象上,则k的值是 ( )
A.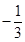 | B.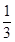 | C.3 | D.-3 |
如图,若点M是x轴正半轴上任意一点,过点M作PQ∥y轴,分别交函数 和
和 的图象于点P和Q,连接OP和OQ.则下列结论正确的是( )
的图象于点P和Q,连接OP和OQ.则下列结论正确的是( )
| A.∠POQ不可能等于90° |
B. |
| C.这两个函数的图象一定关于x轴对称 |
D.△POQ的面积是 |
小兰画了一个函数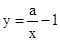 的图象如图,那么关于x的分式方程
的图象如图,那么关于x的分式方程 的解是( )
的解是( )
| A.x=1 | B.x="2" | C.x="3" | D.x="4" |
如图,点 是反比例函数
是反比例函数 (
( 是常数,
是常数,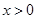 )上的一个动点,过点
)上的一个动点,过点 作
作 轴、
轴、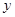 轴的平行线交反比例函数
轴的平行线交反比例函数 (
( 为常数,
为常数, )于点
)于点 、
、 .当点
.当点 的横坐标逐渐增大时,三角形
的横坐标逐渐增大时,三角形 的面积( )
的面积( )
| A.先变大再变小 | B.先变小再变大 | C.不变 | D.无法判断 |
一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系: ,其图象为如图所示的一段曲线,且端点为
,其图象为如图所示的一段曲线,且端点为 和
和 ,若行驶速度不得超过60(km/h),则汽车通过该路段最少需要时间为( )
,若行驶速度不得超过60(km/h),则汽车通过该路段最少需要时间为( )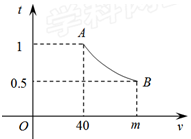
A. 分 分 | B.40分 | C.60分 | D. 分 分 |
下列函数中,y是x的反比例函数的是( )
A.y=﹣ | B.y=﹣ | C.y= | D.y= |