题目内容
【题目】阅读下面的文字,解答问题:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部写出来,于是小明用
的小数部分我们不可能全部写出来,于是小明用![]() 来表示
来表示![]() 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<7<3,即2<
的整数部分是1,将这个数减去其整数部分,差就是小数部分.又例如:∵22<7<3,即2<![]() <3,∴
<3,∴![]() 的整数部分为2,小数部分为
的整数部分为2,小数部分为![]() ﹣2.
﹣2.
请解答:
(1)![]() 的整数部分是 ,小数部分是 .
的整数部分是 ,小数部分是 .
(2)如果![]() 的小数部分为a,
的小数部分为a, ![]() 的整数部分为b,求a+b-
的整数部分为b,求a+b-![]() 的值;
的值;
(3)已知:x是3+![]() 的整数部分,y是其小数部分,请直接写出x﹣y的值的相反数.
的整数部分,y是其小数部分,请直接写出x﹣y的值的相反数.
【答案】(1)3; ![]() ﹣3;(2)4;(3)7﹣
﹣3;(2)4;(3)7﹣![]() ,其相反数是
,其相反数是![]() ﹣7.
﹣7.
【解析】试题分析:(1)求出![]() 的范围是3<
的范围是3<![]() <4,根据题目中所给的方法即可求出答案;
<4,根据题目中所给的方法即可求出答案;
(2)求出![]() 的范围是2<
的范围是2<![]() <3,求出
<3,求出![]() 的范围是6<
的范围是6<![]() <7,根据题目中所给的方法求得a、b的值,再代入求值即可;(3)求出
<7,根据题目中所给的方法求得a、b的值,再代入求值即可;(3)求出![]() 的范围,推出3+
的范围,推出3+![]() 的范围,结合题目中所给的方法求出x、y的值,代入即可.
的范围,结合题目中所给的方法求出x、y的值,代入即可.
试题解析:
(1)![]() 的整数部分是3,小数部分是
的整数部分是3,小数部分是![]() ﹣3;
﹣3;
故答案为:3;![]() ﹣3;
﹣3;
(2)∵4<5<9,
∴2<![]() <3,即a=
<3,即a=![]() ﹣2,
﹣2,
∵36<37<49,
∴6<![]() <7,即b=6,
<7,即b=6,
则a+b﹣![]() =4;
=4;
(3)根据题意得:x=5,y=3+![]() ﹣5=
﹣5=![]() ﹣2,
﹣2,
∴x﹣y=7﹣![]() ,其相反数是
,其相反数是![]() ﹣7.
﹣7.

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案【题目】某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示:
组号 | 分组 | 频数 |
一 | 6≤m<7 | 2 |
二 | 7≤m<8 | 7 |
三 | 8≤m<9 | a |
四 | 9≤m≤10 | 2 |
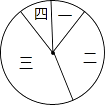
(1)求a的值;
(2)若用扇形图来描述,求分数在8≤m<9内所对应的扇形图的圆心角大小;
(3)将在第一组内的两名选手记为:A1、A2 , 在第四组内的两名选手记为:B1、B2 , 从第一组和第四组中随机选取2名选手进行调研座谈,求第一组至少有1名选手被选中的概率(用树状图或列表法列出所有可能结果).