题目内容
【题目】(1)如图1,线段AC=6cm,线段BC=15cm,点M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长.
(2)如图2,∠BOE=2∠AOE,OF平分∠AOB,∠EOF=20°.求∠AOB.
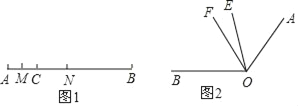
【答案】(1)MN的长为8cm;(2)∠AOB=120°.
【解析】
试题(1)直接利用两点之间距离分别得出CN,MC的长进而得出答案;
(2)直接利用角平分线的性质以及结合已知角的关系求出答案.
试题解析:解:(1)∵M是AC的中点,AC=6cm,∴MC=![]() AC=6×
AC=6×![]() =3cm.
=3cm.
又因为CN:NB=1:2,BC=15cm,∴CN=15×![]() =5cm,∴MN=MC+CN=3+5=8cm,∴MN的长为8cm;
=5cm,∴MN=MC+CN=3+5=8cm,∴MN的长为8cm;
(2)∵∠BOE=2∠AOE,∠AOB=∠BOE+∠AOE,∴∠BOE=![]() ∠AOB.
∠AOB.
∵OF平分∠AOB,∴∠BOF=![]() ∠AOB,∴∠EOF=∠BOE﹣∠BOF=
∠AOB,∴∠EOF=∠BOE﹣∠BOF=![]() ∠AOF.
∠AOF.
∵∠EOF=20°,∴∠AOB=120°.

练习册系列答案
相关题目