题目内容
【题目】如图,在平面直角坐标系中,四边形ABCD为正方形,已知点A(![]() ,0)、D(
,0)、D(![]() ,3),点B、C在第二象限内.
,3),点B、C在第二象限内.
(1)点B的坐标 ;
(2)将正方形ABCD以每秒2个单位的速度沿x轴向右平移t秒,若存在某一时刻t,使在第一象限内点B、D两点的对应点B′、D′正好落在某反比例函数的图像上,请求出此时t的值以及这个反比例函数的解析式;
(3)在(2)的情况下,问是否存在y轴上的点P和反比例函数图像上的点Q,使得以P、Q、B′、D′四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点P、Q的坐标;若不存在,请说明理由.
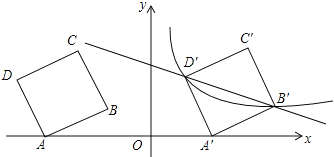
【答案】(1)B(-2,1);(2)t=4,反比例函数解析式为![]() ;
;
(3)当B′D′为对角线时,![]() ,
,![]() ;当B′D′为边时,
;当B′D′为边时,![]() ,
,![]() 或
或![]() ,
,![]()
【解析】分析:(1)过点D作DE⊥x轴于点E,过点B作BF⊥x轴于点F,由正方形的性质结合同角的余角相等即可证出△ADE≌△BAF,从而得出DE=AF,AE=BF,再结合点A、D的坐标即可求出点B的坐标;
(2)设反比例函数为y=![]() ,根据平行的性质找出点B′、D′的坐标,再结合反比例函数图象上点的坐标特征即可得出关于k、t的二元一次方程组,解方程组解得出结论;
,根据平行的性质找出点B′、D′的坐标,再结合反比例函数图象上点的坐标特征即可得出关于k、t的二元一次方程组,解方程组解得出结论;
(3)假设存在,设点P的坐标为(m,0),点Q的坐标为(n,![]() ).分B′D′为对角线或为边考虑,根据平行四边形的性质找出关于m、n的方程组,解方程组即可得出结论.
).分B′D′为对角线或为边考虑,根据平行四边形的性质找出关于m、n的方程组,解方程组即可得出结论.
详解:(1)过点D作DE⊥x轴于点E,过点B作BF⊥x轴于点F,如图1所示.

∵四边形ABCD为正方形,
∴AD=AB,∠BAD=90°,
∵∠EAD+∠ADE=90°,∠EAD+∠BAF=90°,
∴∠ADE=∠BAF.
在△ADE和△BAF中,
 ,
,
∴△ADE≌△BAF(AAS),
∴DE=AF,AE=BF.
∵点A(-6,0),D(-7,3),
∴DE=3,AE=1,
∴点B的坐标为(-6+3,0+1),即(-3,1).
故答案为:(-3,1).
(2)设反比例函数为y=![]() ,
,
由题意得:点B′坐标为(-3+t,1),点D′坐标为(-7+t,3),
∵点B′和D′在该比例函数图象上,
∴k=(-3+t)×1=(-7+t)×3,
解得:t=9,k=6,
∴反比例函数解析式为y=![]() .
.
(3)假设存在,设点P的坐标为(m,0),点Q的坐标为(n,![]() ).
).
以P、Q、B′、D′四个点为顶点的四边形是平行四边形分两种情况:
当B′D′为对角线时,![]() ,
,![]()
当B′D′为边时, ![]() ,
,![]() 或
或![]() ,
,![]()