题目内容
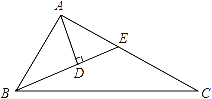
【题目】麒麟区第七中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,CD=13m,AD=12m.

(1)求出空地ABCD的面积?
(2)若每种植1平方米草皮需要300元,问总共需投入多少元?
【答案】(1)36;(2)10800.
【解析】试题分析:连接AC,在Rt△ABC中根据勾股定理可求得AC的长,再由勾股定理的逆定理判定△ACD为直角三角形,根据S四边形ABCD=S△BAC+S△DAC即可求得空地ABCD的面积;(2)在(1)的基础上求解即可.
试题解析:
(1)如图,连接AC,

在Rt△ABC中,AC2=AB2+BC2=32+42=52,
∴AC=5m.
在△ACD中,CD2=132,AD2=122,
而122+52=132,
即AC2+AD2=CD2,
∴∠CAD=90°,
S四边形ABCD=S△BAC+S△DAC=![]() BCAB+
BCAB+![]() ADAC=
ADAC=![]() ×4×3+
×4×3+![]() ×12×5=36(m2).
×12×5=36(m2).
答:空地ABCD的面积为36m2.
(2)所以需费用为:36×300=10800(元).
答:总共需投入10800元.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目