题目内容
【题目】在平面直角坐标系中画出两条相交直线y=x和y=kx+b,交点为(x0 , y0),在x轴上表示出不与x0重合的x1 , 先在直线y=kx+b上确定点(x1 , y1),再在直线y=x上确定纵坐标为y1的点(x2 , y1),然后在x轴上确定对应的数x2 , …,依次类推到(xn , yn-1),我们来研究随着n的不断增加,xn的变化情况.如图1(注意:图在下页上),若k=2,b=—4,随着n的不断增加,xn逐渐(填“靠近”或“远离”)x0;如图2,若k= ![]() ,b=2,随着n的不断增加,xn逐渐(填“靠近”或“远离”)x0;若随着n的不断增加,xn逐渐靠近x0 , 则k的取值范围为 .
,b=2,随着n的不断增加,xn逐渐(填“靠近”或“远离”)x0;若随着n的不断增加,xn逐渐靠近x0 , 则k的取值范围为 . 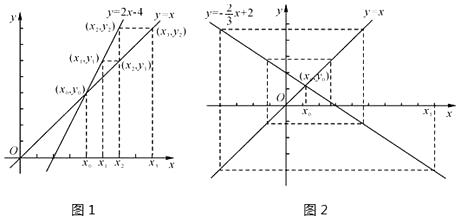
【答案】远离;靠近;-1<k<1且k≠0
【解析】(1)由分析可知第1空填“远离”,(2)第2空填“靠近”;
(3)联立方程组![]() 解得
解得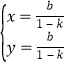
即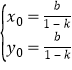 .
.
I.当k>1时,y=kx+b随着x的增大而增大,
则x>x0时kx+b>x
取x1>x0 , 则kx1+b>x1,即y1=kx1+b>x1;
由题意得x2=y1=kx1+b>x1,
同理,x3=y2=kx2+b>x2,
……
xn=yn-1=kxn-1+b>xn-1,
所以得到一组点(x1,y1),(x2,y1),(x2,y2),…,(xn,yn-1) ,
且x0<x1<x2<x3<…<xn,
则k>1时,随着n的不断增加,xn逐渐远离x0;
同理可得,当k<-1时,随着n的不断增加,xn逐渐远离x0
II.当0<k<1时,y=kx+b随着x的增大而增大,
则x>x0时kx+b<x
取x1>x0 , 则x0<kx1+b<x1,即x0=y0<y1=kx1+b<x1;
由题意得x2=y1=kx1+b,则x0<x2<x1,
同理,x3=y2=kx2+b<x2,则x0<x3<x2,
……
xn=yn-1=kxn-1+b<xn-1,则x0<xn<xn-1,
所以得到一组点(x1,y1),(x2,y1),(x2,y2),…,(xn,yn-1) ,
且x0<xn<xn-1<…<x3<x2<x1,
则0<k<1时,随着n的不断增加,xn逐渐靠近x0;
同理可得,当-1<k<0时,随着n的不断增加,xn逐渐靠近x0.
综上-1<k<1且k≠0时,随着n的不断增加,xn逐渐靠近x0.
故答案为-1<k<1且k≠0.
根据图1和图2,观察(xn , yn-1)的位置,
(1)容易看到图1中的(xn , yn-1)与(x0 , y0)越来越远;
(2)容易看到图2中的(xn , yn-1)与(x0 , y0)越来越靠近;
(3)根据图1和图2的例子,可以分k>1,k<-1,0<k<1和-1<k<0分类讨论,求出xn的值变化情况即可.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】某校组织了一次G20知识竞赛活动,根据获奖同学在竞赛中的成绩制成的统计图表如下,仔细阅读图表解答问题: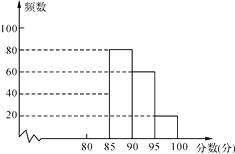
分数段 | 频数 | 频率 |
80≤x<85 | a | 0.2 |
85≤x<90 | 80 | b |
90≤x<95 | 60 | c |
95≤x<100 | 20 | 0.1 |
(1)求出表中a,b,c的数值,并补全频数分布直方图;
(2)获奖成绩的中位数落在哪个分数段?
(3)估算全体获奖同学成绩的平均分.