题目内容
【题目】下列命题:
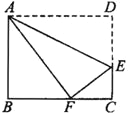
①有一条直角边和斜边的高对应相等的两个直角三角形全等;
②有两边和其中一边上高对应相等的两个三角形全等;
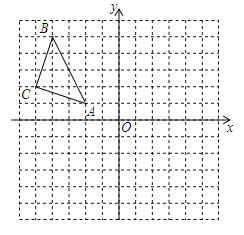
③有两边和第三边上的中线对应相等的两个三角形全等;
④有两边和其中一边上的中线对应相等的两个三角形全等.
其中正确的命题有( )A.1个 B.2个 C.3个 D.4个
【答案】C
【解析】
试题三角形全等的判定方法有AAS,ASA,SAS,SSS,HL,没有SSA,从已知条件入手,结合全等的判定方法,通过分析推理,对结论一个个进行验证.
解:A、一条直角边和斜边上的高对应相等的两个直角三角形全等;根据HL可证得两直角三角形全等,本小题正确;
B、有两边及其中一边上的高对应相等的两个三角形不一定全等,如图:△ABC和△ACD,的边AC=AC,BC=CD,高AE=AE,但△ABC和△ACD不全等,故选项错误;
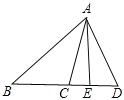
C、可根据SSS证明两个三角形全等,故选项正确;
D、正确,符合SAS.
故选C.

练习册系列答案
相关题目