题目内容
【题目】如图,在△ABC中,AB>AC,AD平分∠BAC
(1)尺规作图:在AD上标出一点P,使得点P到点B和点C的距离相等(不写作法,但必须保留作图痕迹);
(2)过点P作PE⊥AB于点E,PF⊥AC于点F,求证:BE=CF;
(3)若AB=a,AC=b,则BE= ,AE= .

【答案】(1)详见解析;(2)详见解析;(3)![]() ,
,![]() .
.
【解析】
(1)作线段BC 的垂直平分线与AD的交点即为所求.
(2)只要证明△PEB≌△PFC即可.
(3)只要证明△PAE≌△PAF,推出AE=AF,设BE=CF=x,则有a-x=b+x,解方程即可解决问题.
(1)①作线段BC的垂直平分线交AD于P.
点P就是所求的点.
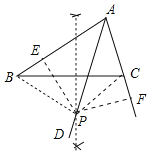
(2)连接PB、PC.
∵∠PAB=∠PAF,PE⊥AB,PF⊥AC,
∴PE=PF,
在Rt△PEB和Rt△PFC中,
![]() ,
,
∴△PEB≌△PFC,
∴BE=CF.
(3)设BE=CF=x,
在Rt∴△PAE和Rt△PAF中,
![]() ,
,
∴△PAE≌△PAF,
∴AE=AF,
∴AB-BE=AC+CF,
∴a-x=b+x,
∴x=![]() ,
,
∴BE=![]() ,AE=AB-BE=a-
,AE=AB-BE=a-![]() =
=![]() ,
,
故答案为![]() ,
,![]() .
.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目