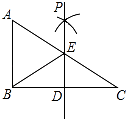题目内容
【题目】如图,已知AD为△ABC的高线,AD=BC,以AB为底边作等腰Rt△ABE,连接ED,EC,延长CE交AD于F点,下列结论:①△ADE≌△BCE;②CE⊥DE;③BD=AF;④S△BDE=S△ACE,其中正确的有( )

A. ①③ B. ①②④ C. ①②③④ D. ①③④
【答案】C
【解析】
①易证∠CBE=∠DAE,即可求证:△ADE≌△BCE;
②根据①结论可得∠AEC=∠DEB,即可求得∠AED=∠BEG,即可解题;
③证明△AEF≌△BED即可;
④易证△FDC是等腰直角三角形,则CE=EF,S△AEF=S△ACE,由△AEF≌△BED,可知S△BDE=S△ACE,所以S△BDE=S△ACE.
①∵AD为△ABC的高线,∴∠CBE+∠ABE+∠BAD=90°.
∵Rt△ABE是等腰直角三角形,∴∠ABE=∠BAE=∠BAD+∠DAE=45°,AE=BE,∴∠CBE+∠BAD=45°,∴∠DAE=∠CBE.在△DAE和△CBE中,∵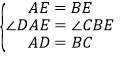 ,∴△ADE≌△BCE(SAS);故①正确;
,∴△ADE≌△BCE(SAS);故①正确;
②∵△ADE≌△BCE,∴∠EDA=∠ECB.
∵∠ADE+∠EDC=90°,∴∠EDC+∠ECB=90°,∴∠DEC=90°,∴CE⊥DE;故②正确;
③∵∠BDE=∠ADB+∠ADE,∠AFE=∠ADC+∠ECD,∴∠BDE=∠AFE.
∵∠BED+∠BEF=∠AEF+∠BEF=90°,∴∠BED=∠AEF.
在△AEF和△BED中,∵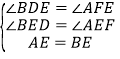 ,∴△AEF≌△BED(AAS),∴BD=AF;故③正确;
,∴△AEF≌△BED(AAS),∴BD=AF;故③正确;
④∵AD=BC,BD=AF,∴CD=DF.
∵AD⊥BC,∴△FDC是等腰直角三角形.
∵DE⊥CE,∴EF=CE,∴S△AEF=S△ACE.
∵△AEF≌△BED,∴S△AEF=S△BED,∴S△BDE=S△ACE.故④正确.
故选C.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案