题目内容
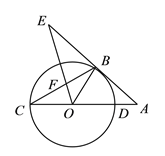
【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
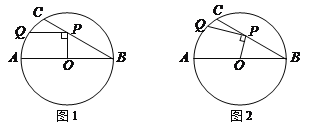
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)在Rt△OPB中,由OP=OB·tan∠ABC可求得OP=![]() ,连接OQ,在Rt△OPQ中,根据勾股定理可得PQ的长;(2)由勾股定理可知
,连接OQ,在Rt△OPQ中,根据勾股定理可得PQ的长;(2)由勾股定理可知![]() OQ为定值,所以当当OP最小时,PQ最大.根据垂线段最短可知,当OP⊥BC时OP最小,所以在Rt△OPB中,由OP=OB·sin∠ABC求得OP的长;在Rt△OPQ中,根据勾股定理求得PQ的长.
OQ为定值,所以当当OP最小时,PQ最大.根据垂线段最短可知,当OP⊥BC时OP最小,所以在Rt△OPB中,由OP=OB·sin∠ABC求得OP的长;在Rt△OPQ中,根据勾股定理求得PQ的长.

试题解析:解:(1)∵OP⊥PQ,PQ∥AB,∴OP⊥AB.
在Rt△OPB中,OP=OB·tan∠ABC=3·tan30°=![]() .
.
连接OQ,在Rt△OPQ中, ![]() .
.
(2) ∵![]()
∴当OP最小时,PQ最大,此时OP⊥BC.
OP=OB·sin∠ABC=3·sin30°=![]() .
.
∴PQ长的最大值为 .
.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目