题目内容
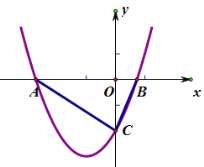
【题目】已知抛物线y=![]() x2-mx+c与x轴交于点A(x1,0)B(x2,0),与y轴交于点C(0,c).若△ABC为直角三角形,求c的值
x2-mx+c与x轴交于点A(x1,0)B(x2,0),与y轴交于点C(0,c).若△ABC为直角三角形,求c的值
【答案】![]() .
.
【解析】
由△ACO∽△CBO可得OC2=OB·OA,由一元二次方程根据系数的关系可得x1·x2=2c,即OB·OA=-2c,从而可得c2+2c=0,解方程即可求出c的值.
解:∵△ABC为直角三角形,
∴∠ACB=90°,
∵∠ACO+∠BCO=90°,∠CBO+∠BCO=90°,
∴∠ACO=∠CBO,
∴△ACO∽△CBO,
∴![]() ,
,
∴OC2=OB·OA.
当y=0时,![]() x2-mx+c=0,
x2-mx+c=0,
∴x1·x2=2c,
∴OB·OA=-2c.
∵C(0,c),
∴OC=-c,
∴(-c)2=-2c,
∴c2+2c=0,
∴c1=0(舍去),c2=-2.
∴c的值是-2.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目