题目内容
【题目】已知:平行四边形![]() ,对角线
,对角线![]() 点P为射线BC上一点,
点P为射线BC上一点,![]() ,(点M与点B分别在直线AP的两侧),且
,(点M与点B分别在直线AP的两侧),且![]() 联结MD.
联结MD.
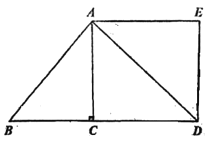
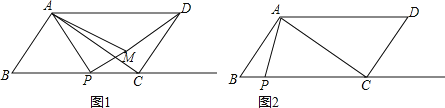
(1)当点M在![]() 内时,如图一,设
内时,如图一,设![]() 求
求![]() 关于
关于![]() 的函数解析式.
的函数解析式.
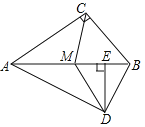
(2)请在图二中画出符合题意得示意图,并探究:图中是否存在与![]() 相似的三角形?若存在,请写出证明过程,若不存在,请说明理由
相似的三角形?若存在,请写出证明过程,若不存在,请说明理由
(3)当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的长.
的长.
【答案】(1) ;(2)
;(2)![]() ,证明见解析;(3)7.5或3或27.
,证明见解析;(3)7.5或3或27.
【解析】
(1)作AE⊥BC于E,先在Rt△ABC中运用勾股定理求出BC=15,再解Rt△ABE,得到AE=![]() ,BE=
,BE=![]() ,然后在Rt△AEP中,利用勾股定理得AP2=PE2+AE2,即可求出y关于x的函数关系式;
,然后在Rt△AEP中,利用勾股定理得AP2=PE2+AE2,即可求出y关于x的函数关系式;
(2)先由两角对应相等的两三角形相似证明出△APM∽△ACD,则AP:AC=AM:AD,即AP:AM=AC:AD,又由∠PAM=∠CAD,得出∠PAC=∠MAD,根据两边对应成比例且夹角相等的两三角形相似即可得到△PAC∽△MAD;
(3)先由相似三角形的形状相同,由(2)得出△APC为等腰三角形,再分两种情况进行讨论:①点M在平行四边形内;②点M在平行四边形外;又分两种情况:(i)P在BC上,(ii)P在BC的延长线上.
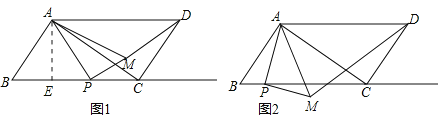
解:(1)如图,作AE⊥BC于E,
在Rt△ABC中,∵AB=9,AC=12,
∴BC=15,
∵△ABE∽△CBA,
∴BE=![]() ,AE=
,AE=![]()
∵BP=![]() ,∴PE=
,∴PE=![]() ,
,
在Rt△AEP中,![]()
∴
(2) 存在,![]() ,
,
∵∠PAM=∠CAD,∠APM=∠ACD=90°,
∴△APM∽△ACD,
∴![]()
∴![]()
∵![]() ,
,
∴∠PAC=∠MAD,
∴![]()
(3)∵△PAC∽△MAD,
∴当△AMD为等腰三角形时,△APC也为等腰三角形,
①当点M在平行四边形内时,如图1.点P只能在EC上,
∵∠APC为钝角,
∴∠PAC=∠PCA,
∴PC=PA,
又∵∠PAB=90°-∠PAC,∠B=90°-∠PCA,
∴∠PAB=∠B,∴PA=PB,
∴PA=PB=PC=![]() BC=
BC=![]() ,
,
即BP=7.5;
②当点M在平行四边形外时,
(i)若P在BC上,如图2.点P只能在BE上,
∵AP<AC,AP<PC,
∴CA=CP=12,则BP=15-12=3;
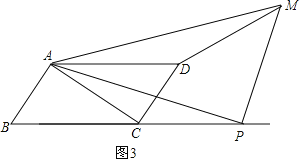
(ii)若P在BC的延长线上,如图3,
∵AP>AC,AP>PC,
∴CA=CP=12,则BP=15+12=27.
综上可知,当△AMD为等腰三角形时,BP的长为7.5或3或27.

 阅读快车系列答案
阅读快车系列答案