题目内容
【题目】关于x的一元二次方程ax2﹣3x﹣1=0的两个不相等的实数根都在﹣1和0之间（不包括﹣1和0），则a的取值范围是 ．
【答案】
＜a＜﹣2
【解析】解：∵关于x的一元二次方程ax2﹣3x﹣1=0的两个不相等的实数根
∴△=（﹣3）2﹣4×a×（﹣1）＞0，
解得：a＞ 
设f（x）=ax2﹣3x﹣1，如图，
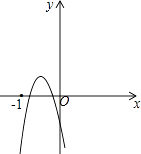
∵实数根都在﹣1和0之间，
∴﹣1 
，
∴a 
，
且有f（﹣1）＜0，f（0）＜0，
即f（﹣1）=a×（﹣1）2﹣3×（﹣1）﹣1＜0，f（0）=﹣1＜0，
解得：a＜﹣2，
∴ ＜a＜﹣2，
所以答案是： ＜a＜﹣2．
【考点精析】掌握抛物线与坐标轴的交点是解答本题的根本，需要知道一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．
练习册系列答案
相关题目
【题目】在《科学》课上，老师讲到温度计的使用方法及液体的沸点时，好奇的王红同学准备测量食用油的沸点，已知食用油的沸点温度高于水的沸点温度（
），王红家只有刻度不超过的温度计，她的方法是在锅中倒入一些食用油，用煤气灶均匀加热，并每隔
测量一次锅中油温，测量得到的数据如下表：
时间 | 0 | 10 | 20 | 30 | 40 |
油温 | 10 | 30 | 50 | 70 | 90 |
王红发现，烧了
时，油沸腾了，则下列说法不正确的是（ ）
A. 没有加热时，油的温度是
B. 加热
，油的温度是
C. 估计这种食用油的沸点温度约是
D. 每加热，油的温度升高
