题目内容
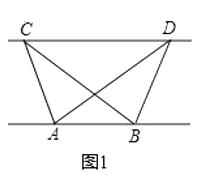
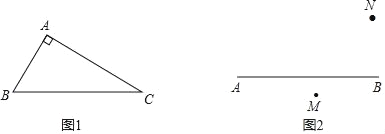
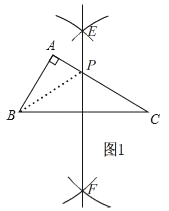
【题目】(1)如图1,在Rt△ABC中,AB=3,AC=4,BC=5,若直线EF垂直平分BC,请你利用尺规画出直线EF;
(2)若点P在(1)中BC的垂直平分线EF上,请直接写出PA+PB的最小值,回答PA+PB取最小值时点P的位置并在图中标出来;
解:PA+PB的最小值为 ,PA+PB取最小值时点P的位置是 ;
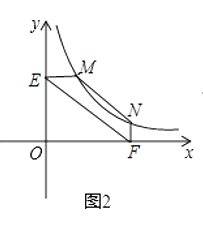
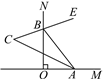
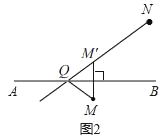
(3)如图2,点M,N分别在直线AB两侧,在直线AB上找一点Q,使得∠MQB=∠NQB.要求画图,并简要叙述确定点Q位置的步骤(无需尺规作图,保留画图痕迹,无需证明)
解:确定点Q位置的简要步骤: .
【答案】(1)见解析;(2)4,直线EF与边AC的交点;(3)见解析.
【解析】
(1)根据线段垂直平分线的作法即可得出结论;
(2)利用线段的垂直平分线的性质即可得出结论;
(3)利用对称性先确定出点M关于直线AB的对称点,过点M'作射线NM'交直线AB于Q,即可得出结论.
(1)如图1所示,
(2)∵点P是BC的垂直平分线EF上,
∴BP=PC,
∴PA+PB=PA+PC,
∴点P在边AC上时,PA+PC最小,AC=4,
故答案为:4,直线EF与AC边的交点;
(3)如图2,①作点M关于直线AB的对称点M',
②过点M'作射线NM'交直线AB于Q,
③连接MQ,则∠MQB=∠NQB,
即:点Q就是所求作的点,
故答案为:①作点M关于直线AB的对称点M',②过点M'作射线NM'交直线AB于Q,③连接MQ,即:点Q就是所求作的图.

练习册系列答案
相关题目
【题目】某同学在用描点法画二次函数y= ![]() +bx+c的图象时,列出了下面的表格:
+bx+c的图象时,列出了下面的表格:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣11 | ﹣2 | 1 | ﹣2 | ﹣5 | … |
由于粗心,他算错了其中一个y值,则这个错误的数值是( ).
A.﹣11 B.﹣2 C.1 D.﹣5