题目内容
【题目】已知:如图,D是BC上一点,△ABC∽△ADE,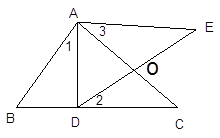
求证:∠1=∠2=∠3 .
【答案】证明:∵△ABC∽△ADE,
∴∠BAC=∠DAE,∠C=∠E,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠1=∠3,
又∵∠C=∠E,∠DOC=∠AOE,
∴△DOC∽△AOE,
∴∠2=∠3 ,
∴∠1=∠2=∠3
【解析】由△ABC∽△ADE,得到对应角相等,得到△DOC∽△AOE,得到∠1=∠2=∠3.
【考点精析】掌握相似三角形的判定与性质是解答本题的根本,需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目
【题目】某公交车每月的支出费用为4000元,票价为2元/人,设每月有![]() 人乘坐该公交车,每月利润为
人乘坐该公交车,每月利润为![]() 元(利润=收入-支出).
元(利润=收入-支出).
(1)请写出![]() 与
与![]() 的关系式 ;
的关系式 ;
(2)完成表格.
| 500 | 1000 | 1500 | 2000 | 2500 | 3000 | … |
|
|
|
|
|
|
| … |
(3)观察表中数据,每月乘客量达到 人以上时,该公交车才不会亏损.