题目内容
【题目】为更新果树品种，某果园计划新购进A、B两个品种的果树苗栽植培育，若计划购进这两种果树苗共45棵，其中A种树苗的单价为7元/棵，购买B种苗所需费用y（元）与购买数量x（棵）之间存在如图所示的函数关系．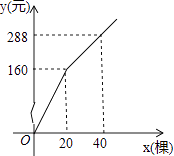
（1）求y与x的函数关系式；
（2）若在购买计划中，B种树苗的数量不超过35棵，但不少于A种树苗的数量，请设计购买方案，使总费用最低，并求出最低费用．
【答案】
（1）解：设y与x的函数关系式为：y=kx+b，
当0≤x≤20时，把（0，0），（20，160）代入y=kx+b中，
得： 
，解得： 
，
此时y与x的函数关系式为y=8x；
当20≤x时，把（20，160），（40，288）代入y=kx+b中，
得： 
，解得： 
，
此时y与x的函数关系式为y=6.4x+32．
综上可知：y与x的函数关系式为y= 
（2）解：∵B种苗的数量不超过35棵，但不少于A种苗的数量，
∴ 
，
∴22.5≤x≤35，
设总费用为W元，则W=6.4x+32+7（45﹣x）=﹣0.6x+347，
∵k=﹣0.6，
∴y随x的增大而减小，
∴当x=35时，W总费用最低，W最低=﹣0.6×35+347=326（元）
【解析】（1）0≤x≤20时，y是x的正比例函数，设y=kx，将点（20,160）代入计算即可，当20≤x时，y是x的一次函数将把（20，160），（40，288）代入y=kx+b求解即可；
（2）依据B种苗的数量不超过35棵，但不少于A种苗的数量列出关于x的不等式组可求得x的取值范围，然后依据总费用W与x之间函数关系式，最后依据一次函数的性质求解即可.
练习册系列答案
阅读快车系列答案
相关题目
