题目内容
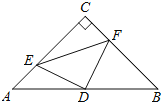
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,D是AB的中点,点E、F分别在AC、BC边上运动
,D是AB的中点,点E、F分别在AC、BC边上运动![]() 点E不与点A、C重合
点E不与点A、C重合![]() ,且保持
,且保持![]() ,连接DE、DF、
,连接DE、DF、![]() 在此运动变化的过程中,有下列结论:
在此运动变化的过程中,有下列结论:![]() ;
;![]() 四边形CEDF的面积随点E、F位置的改变而发生变化;
四边形CEDF的面积随点E、F位置的改变而发生变化;![]() ;
;![]() 以上结论正确的是______
以上结论正确的是______![]() 只填序号
只填序号![]() .
.
【答案】![]()
【解析】
连接CD![]() 证明
证明![]() ,利用全等三角形的性质一一判断即可.
,利用全等三角形的性质一一判断即可.
解:连接CD,
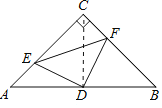
∵△ABC是等腰直角三角形,D是AB的中点,
∴![]() ,CD⊥AB,
,CD⊥AB,
又∵![]() ,
,
∴ ∠ADE=∠CDF=90°-∠EDC,
在△ADE和△CDF中,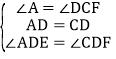 ,
,
∴![]() (ASA)
(ASA)
∴ ED=DF,故①正确;
∴ ![]() ,
,
![]()
![]() 定值,故②错误,
定值,故②错误,
∵![]() ,
,
∴ AE=CF,
∴![]() ,故③正确,
,故③正确,
∵ AE=CF,AC=BC,
∴ EC=BF,
∴![]() ,
,
∵![]() ,
,
∴![]() ,故④正确.
,故④正确.
故答案为:①③④.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
【题目】某同学在用描点法画二次函数y= ![]() +bx+c的图象时,列出了下面的表格:
+bx+c的图象时,列出了下面的表格:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | ﹣11 | ﹣2 | 1 | ﹣2 | ﹣5 | … |
由于粗心,他算错了其中一个y值,则这个错误的数值是( ).
A.﹣11 B.﹣2 C.1 D.﹣5
【题目】某公交车每月的支出费用为4000元,票价为2元/人,设每月有![]() 人乘坐该公交车,每月利润为
人乘坐该公交车,每月利润为![]() 元(利润=收入-支出).
元(利润=收入-支出).
(1)请写出![]() 与
与![]() 的关系式 ;
的关系式 ;
(2)完成表格.
| 500 | 1000 | 1500 | 2000 | 2500 | 3000 | … |
|
|
|
|
|
|
| … |
(3)观察表中数据,每月乘客量达到 人以上时,该公交车才不会亏损.